V. SYNTHETIC METHOD (cont.)

34. On Reduction of Observations of High and Low Water [Footnote 369-3]

A continuous register of the tide or observation at fixed intervals of time, such as each hour, is certainly the best; but for the adequate use of such a record some plan analogous to harmonic analysis is necessary. Observations of high and low water only have, at least until recently, been more usual. Some care has to be taken with respect to these observations, for about high and low water an irregularity in the rise and fall becomes very noticeable, especially if the place of observation is badly chosen. [Footnote 369-4] Observations should therefore be taken every five or ten minutes for half an hour or an hour, embracing the time of high and low water. The time and height of high and low water should then be found by plotting down a curve of heights, and by taking as the true tide-curve a line which presents a sweeping curvature and smoothes away the minor irregularities. A similar but less elaborate process would render hourly observations more perfect. In the reduction the immediate object is to connect, the times and heights of high and low water with the moon’s transits by means of the establishment, age, and fortnightly inequality in the interval and height. The reference of the tide to the establishment is not, however scientifically desirable, and it is better to determine the mean establishment, which is the mean interval from the moon’s transit to high water at spring tide, and the age of the tide, which is the mean period from full moon and change of moon to spring tide.

FIG. 3. -- Tide-curve for Bombay from the beginning of the civil year 1884 to the midnight ending Jan. 14, 1884, or from 12h Dec. 31, 1883, to 12h Jan 14, 1884, astronomical time.
(Click here to see much larger version of this image)

For these purposes the observations may be conveniently treated graphically. [Footnote 369-5] An equally divided horizontal scale is taken to represent the twelve hours of the clock of civil time, regulated to the time of the port, or—more accurately—arranged always to show apparent time by being fast or slow by the equation of time; this time-scale represents the time-of-clock of the moon’s transit, either upper or lower. The scale is perhaps most conveniently arranged in the order V, VI, . . ., XII, I ... IIII. Then each interval of time from transit to high water is set off as an ordinate above the corresponding time-of-clock of the moon’s transit. A sweeping curve is drawn nearly through the tops of the ordinates, so as to cut off minor irregularities. Next along the same ordinates are set off lengths corresponding to the height of water at each high water. A second similar figure may be made for the interval and height at low water. [Footnote 370-1] In the curve of high-water intervals the ordinate corresponding to XII is the establishment, since it gives the time of high water at full moon and change of moon. That ordinate of high-water intervals which is coincident with the greatest ordinate of high-water heights gives the mean establishment. Since the moon’s transit falls about fifty minutes later on each day, in setting off a fortnight’s observations there will be about five days for each four times-of-clock of the upper transit. Hence in these figures we may regard each division of the time-scale I to II, II to III, &c., as representing twenty-five hours instead of one hour. Then the distance from the greatest ordinate of high-water heights to XII is called the age of the tide. From these two figures the times and heights of high and low water may in general be predicted with fair approximation. We find the time-of-clock of the moon’s upper or lower transit on the day, correct by the equation of time, read off the corresponding heights of high and low water from the figures, and the intervals being also read off are added to the time of the moon’s transit and give the times of high and low water. At all ports there is, however, an irregularity of heights and intervals between successive tides, and in consequence of the curves present more or less of a zigzag appearance. Where the zigzag is perceptible to the eye, the curves must be smoothed by drawing them so as to bisect the zigzags, because these diurnal inequalities will not present themselves similarly in the future. When, as in some equatorial ports, the diurnal tides are large, this method of tidal prediction fails.

This method of working out observations of high and low water was not the earliest. In the Mécanique Céleste bks. i and v., Laplace treats a large mass of tidal observations by dividing them into classes depending on the configurations of the tide-generating bodies. Thus he separates the two syzygial tides at full moon and change of moon and divides them into equinoctial and solstitial tides. He takes into consideration the tides of several days embracing these configurations. He goes through the tides at quadratures on the same general plan. The effects of declination and parallax and the diurnal inequalities are similarly treated. Lubbock (Phil. Trans., 1831 sq.) improved the method of Laplace by taking into account all the observed tides, and not merely those appertaining to certain configurations. He divided the observations into a number of classes. First, the tides are separated into parcels, one for each month; then each parcel is sorted according to the hour of the moon’s transit. Another classification is made according to declination; another according to parallax; and a last for the diurnal inequalities. This plan was followed in treating the tides of London, Brest, St Helena, Plymouth, Portsmouth, and Sheerness. Whewell (Phil. Trans., 1834 sq.) did much to reduce Lubbock’s results to a mathematical form, and made a highly important advance by the introduction of graphical methods by means of curves. The method explained above is due to him. Airy remarks of Whewell’s papers that they appear to be "the best specimens of reduction of new observations that we have ever seen."

Footnotes

369-3 Founded on Whewell’s article "Tides", in Admiralty Sc. Manual (ed. 1841), and on Airy’s "Tides and Waves," in Ency. Metrop.

369-4 Waves with a period of from five to twenty minutes are very common, and appear to be analogous to the "seiches" of Geneva and other lakes. See Forel, Bulletin Soc. Vaud. Sci. Nat., 1873, 1875, 1877, and 1879; Ann. Chimie et Physique, vol. ix., 1876; Comptes Rendus, 1879; Arch. Sci., Ph., et Nat., Geneva, 1885; also Airy, "On the Tides of Malta," Phil. Trans., 1878., 1878, part i.

369-5 For a numerical treatment, see Directions for Reducing Tidal Observations, by Commander Burdwood, R.N., London, 1876.

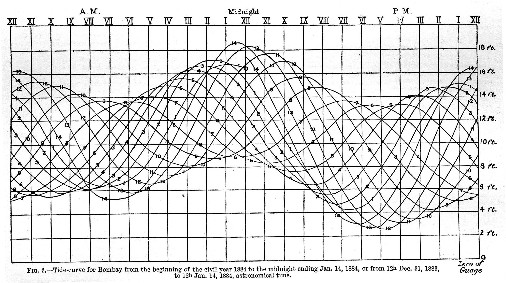
370-1 An example of this kind of curve for the high-water heights for Bombay, drawn automatically by a tide-gauge, would be shown by joining all the high waters together (as in fig. 3) by a continuous curve; and a similar curve may be constructed for the low waters. In this case, however the hours of the clock are repeated twice over, so that the morning and evening tides occur in different halves of the figure, and the hours are not hours of the moon’s transit, but the actual times of high water. It is obvious that the separation of the morning and evening tides prevents the occurrence of the zigzags referred to.






Read the rest of this article:
Tides - Table of Contents