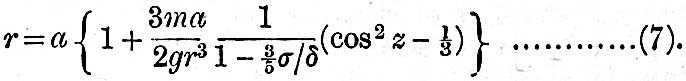1902 Encyclopedia > Tides > [Tide-Generating Forces] Form of Equilibrium
Tides
(Part 6)
II. TIDE-GENERATING FORCES (cont.)
6. Form of Equilibrium
Let us consider the shape assumed by a layer of fluid of density σ, lying on a globe of mass M, when acted on by disturbing forces whose potential is
Suppose the layer to be very thin, and that the mean radius of the layer is a, and let the equation to the boundary of the fluid be
We assume this form, because the theory of harmonic analysis tells us that the departure from sphericity must be represented by a function of the form
That theory also gives us as the potential of a layer of matter of depth
and density σ, at an external point the value
Hence the whole potential, outside of and up to the fluid layer is
The first term of (5) is the potential of the globe, the second that of the disturbing force, and the third the potential due to departure from sphericity.
Now the fluid must stand in a level surface; hence, if we equate this potential to a constant, we must get back to the equation (4), which was assumed to be that of the surface. In other words, if we put
in (5), the result must be constant, provided the departure from sphericity is small. In effecting the substitution for ρ, we may put ρ = a in the small terms, but in the first term of (5) we put
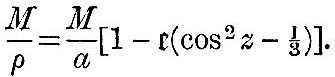
The whole potential (5) can only be constant if, after this substitution, the coefficient of
vanishes. Thus we must have
But if δ be the mean density of the planet
and gravity g = M/a2. Then we easily find that

Form of Equilibrium
Thus the equation to the surface is
If σ be small compared with δ, the coefficient is 3ma/2gr3; thus we see that
is the coefficient by which the mutual attraction of the fluid augments the deformation of the fluid under the action of the disturbing force. If the density of the fluid be the same as that of the sphere, the augmenting factor becomes
which gives the form of equilibrium of a fluid sphere under the action of these forces. Since
it follows that, when the form of equilibrium is
the potential of the forces is
More generally, if we neglect the attraction of the fluid on itself, so that σ/δ is treated as small, and if ρ = α(1 + ς) be the equation to the surface of the fluid, where σ is a function of latitude and longitude, then the potential of the forces under which this is an equilibrium form is
Tide-Generating Force Specified by Equilibrium
It thus appears that we may specify any tide-generating forces by means of the figure of equilibrium which the fluid would assume under them, and in the theory of the tides it has been found practically convenient to specify the forces in this way.
By means of the principle of "forced vibrations" referred to in the historical sketch, we shall pass from the equilibrium form to the actual oscillations of the sea.
Read the rest of this article:
Tides - Table of Contents
|