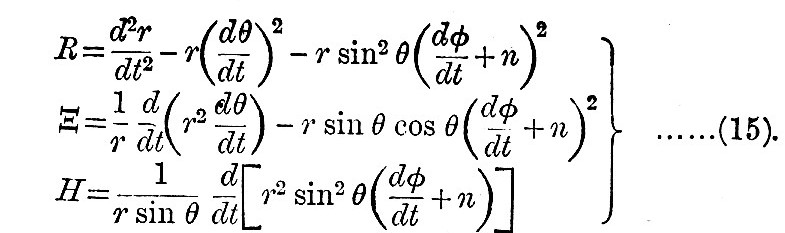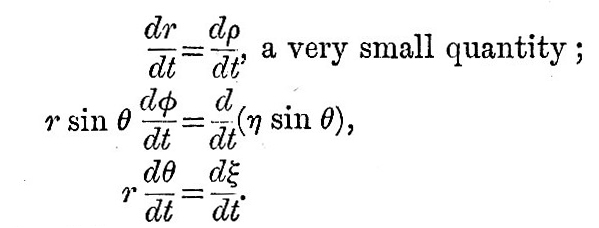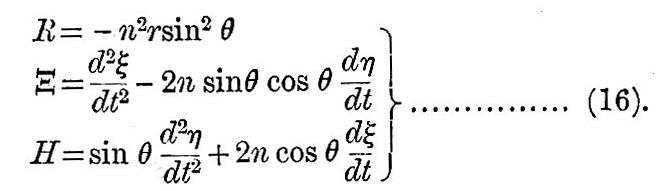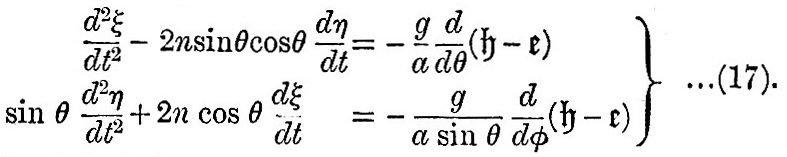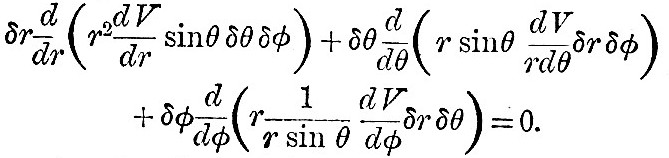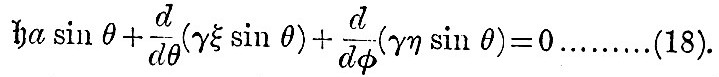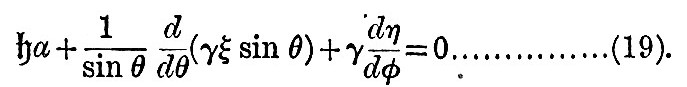1902 Encyclopedia > Tides > [Dynamical Theory of Tides] Equations of Motion
Tides
(Part 11)
III. DYNAMICAL THEORY OF TIDES (cont.)
11. Equations of Motion
Let r, θ, φ be the radius vector, co-latitude, and east longitude of a point with reference to an origin, a polar axis, and a zero-mendian rotating with a uniform angular velocity n from west to east. Then, if R, H, Ξ be the radial, co-latitudinal, and longitudinal accelerations of the point, we have
Now suppose that the point never moves far from a zero position and that its displacements ξ, η sin θ co-latitudinally and longitudinally are very large compared with its radial displacement ρ, and that the velocities are so small that their squares and products are negligible compared with n2r2 ; then we have
Hence (15) is approximately
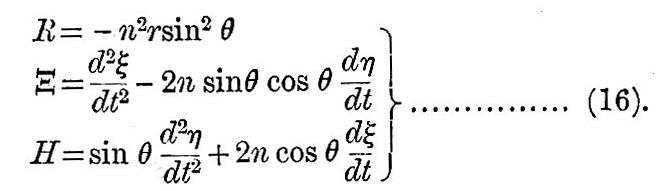
With regard to the first equation of (16), we observe that the time has disappeared, and that R has exactly the same form as if the system were rendered statical by introducing a potential 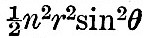 and annulling the rotation of the axes. Since inertia plays no sensible part radially, it follows that, if we apply these expressions to the formation of equations of motion for the ocean, the radial motion need not be considered. We are left, therefore, with only the last two equations of (16). and annulling the rotation of the axes. Since inertia plays no sensible part radially, it follows that, if we apply these expressions to the formation of equations of motion for the ocean, the radial motion need not be considered. We are left, therefore, with only the last two equations of (16).
We now have to consider the forces by which an element of the ocean is urged in the direction of co-latitude and longitude. These forces are those due to the external disturbing forces and to the pressure of the surrounding fluid, the attraction of the fluid on itself being supposed negligible. We have seen in (9) that, if fluid on a sphere of radius a be under the action of disturbing forces whose potential is Ur2, and if 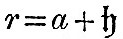 be the equation to the surface, then must be the equation to the surface, then must 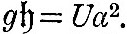 . Hence, if . Hence, if 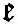 be the equilibrium height of tide, the potential of the disturbing force is be the equilibrium height of tide, the potential of the disturbing force is 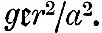 . But, if the elevation be . But, if the elevation be 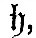 the potential under which it would be in equilibrium is the potential under which it would be in equilibrium is 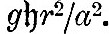 . Therefore, if . Therefore, if 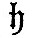 be the elevation of the tide in our dynamical problem, the forces due to hydrostatic pressure on an element of the ocean are the same as would be caused by a potential be the elevation of the tide in our dynamical problem, the forces due to hydrostatic pressure on an element of the ocean are the same as would be caused by a potential 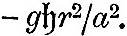 . Hence it follows that the whole forces on the element are those due to a potential . Hence it follows that the whole forces on the element are those due to a potential 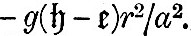 . Therefore from (16) we see that the equations of motion are . Therefore from (16) we see that the equations of motion are
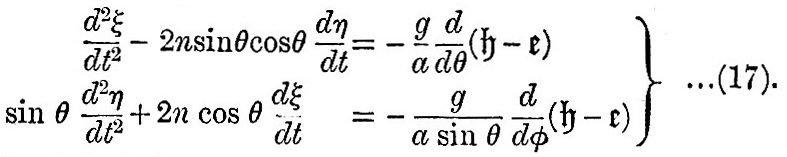
It remains to find the equation of continuity. This may be deduced geometrically from the consideration that the volume of an element of the fluid remains constant; but a shorter way is to derive it from the equation of continuity as it occurs in ordinary hydrodynamical investigations. If V be a velocity potential, the equation of continuity for incompressible fluid is
The element referred to in this equation is defined by r, θ, φ, r + δr, θ + θ, φ + δφ. The co-latitudinal and longitudinal velocities are the same for all the elementary prism defined by θ, φ, θ + δθ, φ + δφ, and the sea bottom. Then
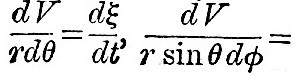
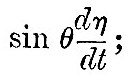 ; ;
This is the equation of continuity, and, together with (17), it forms the system which must be integrated in the general problem of the tides. The difficulties in the way of a solution are so great that none has hitherto been found, except on the supposition that γ, the depth of the ocean, is only a function of latitude. In this case (18) becomes
|