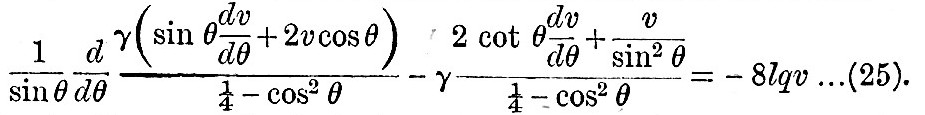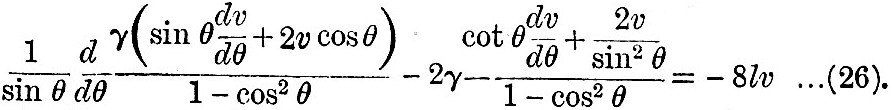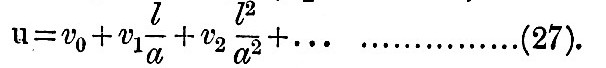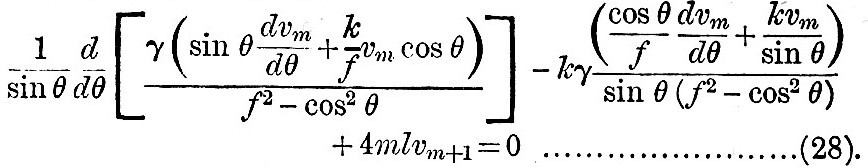1902 Encyclopedia > Tides > [Dynamical Theory of Tides] Preparation for Solution
Tides
(Part 13)
III. DYNAMICAL THEORY OF TIDES (cont.)
13. Preparation for Solution
The ocean which is considered in this case is not like that on the earth’s surface, and therefore it does not seem desirable to pursue the integration of (24) except in certain typical cases.
In (13) we have the expansion of the disturbing potential and implicitly of the disturbing forces in three terms, the first of which is variable in half a day, the second in a day, and the third in half the period of revolution of the tide-raising body. Forestalling the results of chapter iv.—each of these terms may be expressed as the sum of a series of strictly harmonic functions of the time; the first set of these have all approximately semi-diurnal periods, the second approximately diurnal periods, and the third vary slowly in dependence on the periodic time of the tide-generating body. The first set involve twice the terrestrial longitude, the second the longitude, and the third set are independent of the longitude of the place of observation. From these statements compared with (13) we see that in the semi-diurnal terms f is approximately unity, k = 2, and 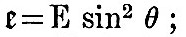 ; in the diurnal terms f is approximately ; in the diurnal terms f is approximately 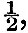 , k = 1, and , k = 1, and 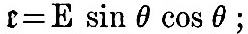 ; in the terms of long period f is a small fraction (for the fortnightly tide about ; in the terms of long period f is a small fraction (for the fortnightly tide about 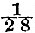 ), k=0, ), k=0, 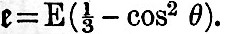 The departure from exactness in the relation f = 1 for the semi-diurnal, and The departure from exactness in the relation f = 1 for the semi-diurnal, and 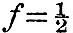 for the diurnal terms is generally (except for certain critical depths of ocean) not such as to greatly change the nature of the results from those obtained when f = 1 and for the diurnal terms is generally (except for certain critical depths of ocean) not such as to greatly change the nature of the results from those obtained when f = 1 and 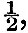 rigorously. Hence the integration of (24) will be pursued on these three hypotheses, giving Laplace’s three kinds of oscillation. The hypothesis which will be made with regard to γ is that γ = l(1 - q cos2 θ), and in the case of the semi-diurnal tides we shall be compelled by mathematical difficulties to suppose q to be either unity or zero. The tides of zonal seas may be worked out, and more complex laws of depth may be assumed; but for the discussion of such cases the reader is referred to Thomson’s papers in Phil. Mag., 1875. rigorously. Hence the integration of (24) will be pursued on these three hypotheses, giving Laplace’s three kinds of oscillation. The hypothesis which will be made with regard to γ is that γ = l(1 - q cos2 θ), and in the case of the semi-diurnal tides we shall be compelled by mathematical difficulties to suppose q to be either unity or zero. The tides of zonal seas may be worked out, and more complex laws of depth may be assumed; but for the discussion of such cases the reader is referred to Thomson’s papers in Phil. Mag., 1875.
There might be reason to conjecture that the form of u would be similar to that of e, and this is in fact the case for the diurnal tides for any value of q and for the semi-diurnal tides when q is unity. Before proceeding further it will be convenient to exhibit two purely analytical transformations of the first two terms of (24) which hold true for certain values of k and f, and when u has such a form as that suggested. If we put k = 1, 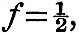 , γ = l(1-q cos2 θ), then, if υ = A sin θ cos θ, it will be found on substitution that , γ = l(1-q cos2 θ), then, if υ = A sin θ cos θ, it will be found on substitution that
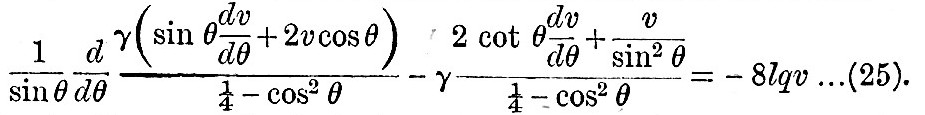
Again, if we put k=2, f=1, q=1, γ = l(1 - cos2 θ) = l sin2 θ, and if υ = A sin2 υ,
Another general property of (24) is derived from the supposition that u is expressed in a series proceeding by powers of l; thus
Let υ0, υ1, υ2, &c., be so chosen that, when u is substituted in (24), the coefficient of each power of l vanishes independently; then the term independent of l obviously gives υ0 = - e, and the connexion between successive υ’s is
We shall suppose below that u is expansible in the form (27), and shall use (28) in conjunction with (25) or (26) for finding the successive values of the υ’s.
Read the rest of this article:
Tides - Table of Contents
|