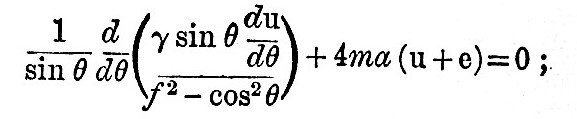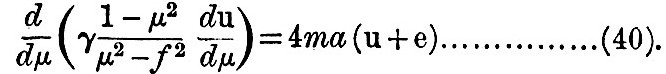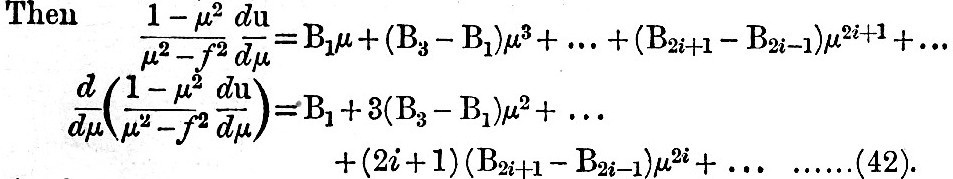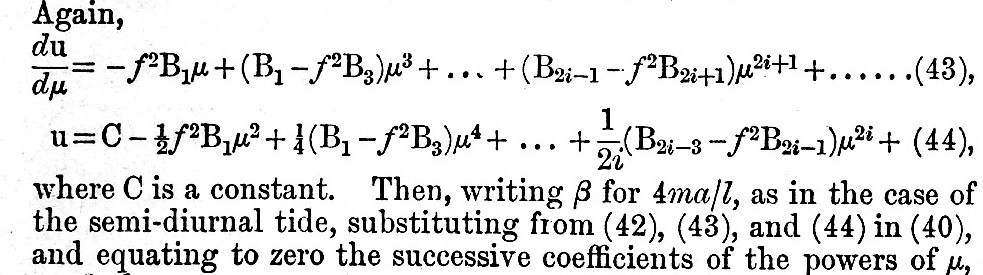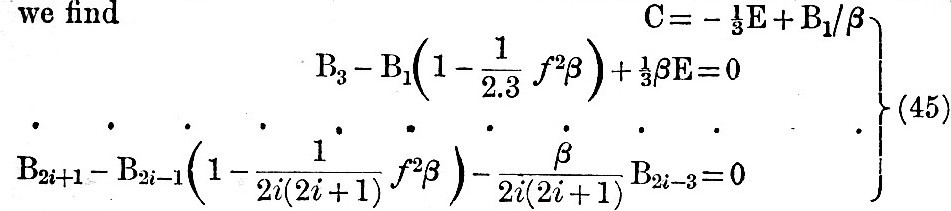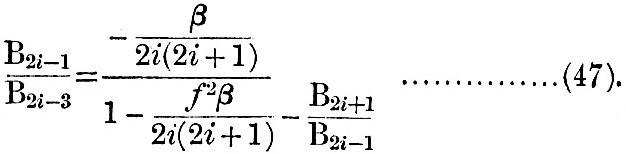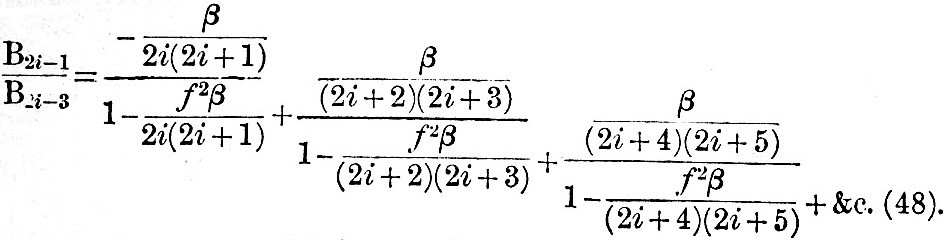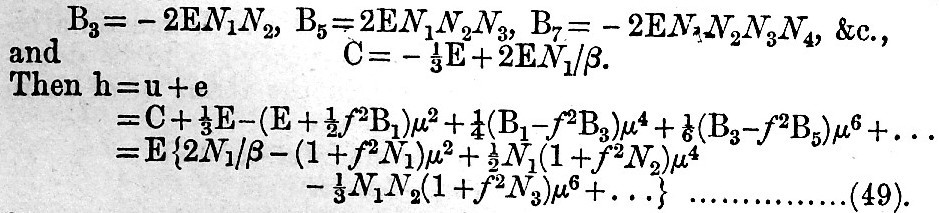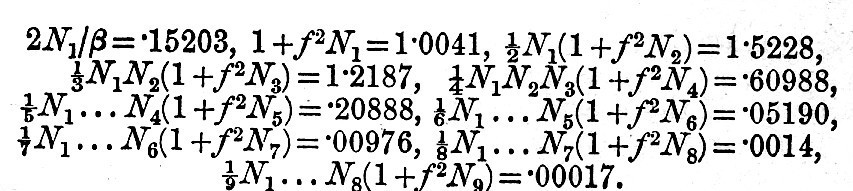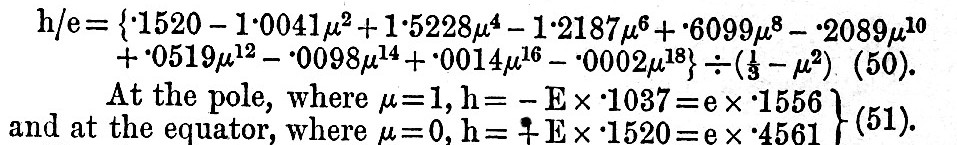III. DYNAMICAL THEORY OF TIDES (cont.)
18. Tides of Long Period in an Ocean of Uniform Depth
As it seems certain that these tides do not satisfy even approximately the equilibrium law, we now proceed to find the solution where there is no friction. In the case of these tides k= 0, f a small fraction, and 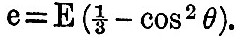 . The equation (24) then becomes
. The equation (24) then becomes
or, writing μ for cos θ and 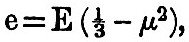
We shall confine the investigation to the case where γ = l, a constant, and where the sea covers the whole surface of the globe. The symmetry of the motion in this case demands that u when expanded in a series of powers of μ shall only involve even powers. Let us assume, therefore, that
Thus the constant C and B3, B5, &c., are all expressible in terms of B1, and B1 is apparently indeterminate. We may remark that, if
the equation of condition (45) may be held to apply for all values of i, from one to infinity. Let us write (45) in the form
When i is large B2i+1/B2i-1 either tends to become infinitely small or it does not do so. Let us suppose that it does not tend to become infinitely small. Then it is obvious that the successive B’s tend to become equal to one another, and so also do the values of (B2i-2-f2B2i-1) /2i and the coefficients of du/dμ. Hence we have du/dμ = L + M/(1-μ2) for all values of μ, where L and M are finite. Hence this hypothesis gives infinite velocity to the fluid at the pole, where μ = 1. But with a water-covered globe this infinite velocity is impossible, and therefore the hypothesis is negatived, and B2i+1/B2i-1 must tend to become infinitely small. This being established, let us write (46) in the form
By repeated applications of (47), we have in the form of a continued fraction
And we know that this is a continuous approximation, which must hold in order to satisfy the condition that the water covers the whole globe. Let us denote this continued fraction by - Ni. Then, if we remember that B-1 = - 2E, we have
B1=2EN1, B3/B1 = - N2, B5/B3 = - N3, B7/B5 = - N4, &c.,
Now we find that, when β = 40, which makes the depth of the sea 3000 fathoms or 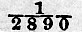 of the radius of the earth, and with f = .0365012, which is the value for the fortnightly tide (see chap. iv.),
of the radius of the earth, and with f = .0365012, which is the value for the fortnightly tide (see chap. iv.),
Now let us take a second case, where β = 10, which was also one of those solved for the case of the semi-diurnal tide by Laplace, and we find
h/E = .2363 - .10016μ2 + .5910μ4 - .1627μ6 + .0258μ8 - .0026μ10 + .0002μ12
At the pole, where μ = l, we find h = - E x .3137 = e x .471, and at the equator h = + E x .2363 = e x .709. With a deeper ocean we should soon arrive at the equilibrium value for the tide, for N1, N2, &c., become very small, and 2N1/β becomes equal to 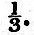 . In this case, with such oceans as those with which we have to deal, the tides of long period are considerably smaller than the equilibrium value.
. In this case, with such oceans as those with which we have to deal, the tides of long period are considerably smaller than the equilibrium value.
Read the rest of this article:
Tides - Table of Contents