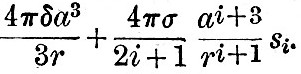1902 Encyclopedia > Tides > [Dynamical Theory of Tides] Stability of the Ocean
Tides
(Part 19)
III. DYNAMICAL THEORY OF TIDES (cont.)
19. Stability of the Ocean
Imagine a globe of density δ, surrounded by a spherical layer of water of density σ. Then, still maintaining the spherical figure, and with water still covering the nucleus, let the layer be displaced sideways. The force on any part of the water distant r′ from the centre of the water and r from the centre of the nucleus is 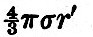 towards the centre of the fluid sphere and towards the centre of the fluid sphere and 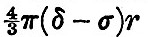 towards the centre of the nucleus. If δ be greater than σ there is a force tending to carry the water from places where it is deeper to places where it is shallower; and therefore the equilibrium, thus arbitrarily disturbed, is stable. If, however, δ is less than σ (or the nucleus lighter than water) the force is such that it tends to carry the water from where it is shallower to where it is deeper, and therefore the equilibrium of a layer of fluid distributed over a nucleus lighter than itself is unstable. As Sir William Thomson has remarked,[Footnote 361-1] if the nucleus is lighter than the ocean, it will float in the ocean with part of its surface dry. Suppose, again, that the fluid layer be disturbed, so that its equation is r = a(1+si), where si is a surface harmonic of degree i ; then the potential due to this deformation is towards the centre of the nucleus. If δ be greater than σ there is a force tending to carry the water from places where it is deeper to places where it is shallower; and therefore the equilibrium, thus arbitrarily disturbed, is stable. If, however, δ is less than σ (or the nucleus lighter than water) the force is such that it tends to carry the water from where it is shallower to where it is deeper, and therefore the equilibrium of a layer of fluid distributed over a nucleus lighter than itself is unstable. As Sir William Thomson has remarked,[Footnote 361-1] if the nucleus is lighter than the ocean, it will float in the ocean with part of its surface dry. Suppose, again, that the fluid layer be disturbed, so that its equation is r = a(1+si), where si is a surface harmonic of degree i ; then the potential due to this deformation is 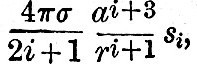 , and the whole potential is , and the whole potential is
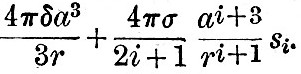
If , therefore, σ/(2i + 1) is greater than 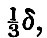 the potential of the forces due to deformation is greater than that due to the nucleus. But we have seen that a deformation tends to increase itself by mutual attraction, and therefore the forces are such as to increase the deformation. If, therefore, the potential of the forces due to deformation is greater than that due to the nucleus. But we have seen that a deformation tends to increase itself by mutual attraction, and therefore the forces are such as to increase the deformation. If, therefore, 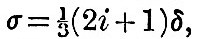 all the deformations up to the ith are unstable, but the i + 1th is stable.[Footnote 361-2] If, however, σ be less than δ, then all the deformations of any order are such that there are positive forces of restitution. For our present purpose it suffices that this equilibrium is stable when the fluid is lighter than the nucleus. all the deformations up to the ith are unstable, but the i + 1th is stable.[Footnote 361-2] If, however, σ be less than δ, then all the deformations of any order are such that there are positive forces of restitution. For our present purpose it suffices that this equilibrium is stable when the fluid is lighter than the nucleus.
Footnotes
361-1 Thomson and Tait, Nat. Phil., § 816.
361-2 Compare an important paper by Poincaré, in Acta Math. (1885), 7; 3, 4.
Read the rest of this article:
Tides - Table of Contents
|