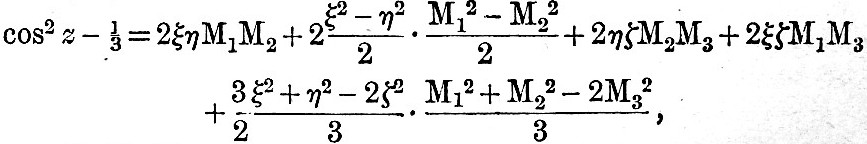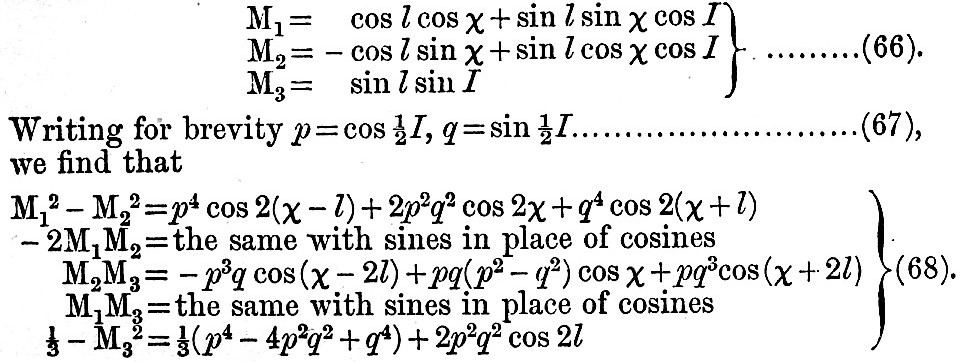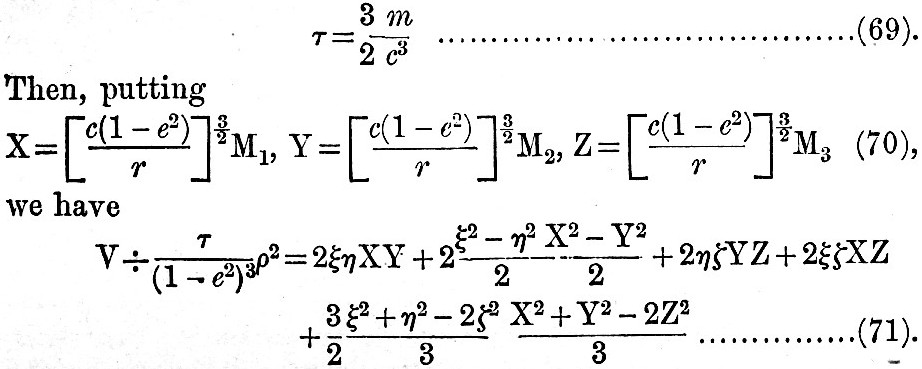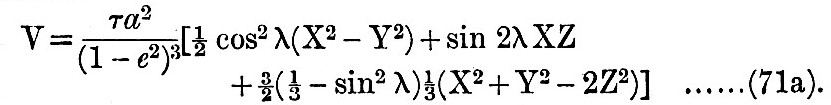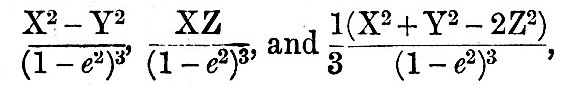1902 Encyclopedia > Tides > [Harmonic Analysis] Development of Equilibrium Theory of Tides in Terms of the Elements of the Orbits
Tides
(Part 23)
IV. HARMONIC ANALYSIS (cont.)
23. Development of Equilibrium Theory of Tides in Terms of the Elements of the Orbits
Within the limits at our disposal we cannot do more than indicate the processes to be followed in this development.
We have already seen in (3) that the expression for the moon’s tide-generating potential is
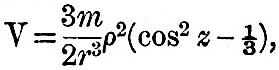
where M1, M2, M3 are the direction cosines of the moon referred to axes fixed in the earth. We require to find the functions 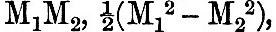 ; &c., of the moon’s direction cosines. [Footnote 363-2] ; &c., of the moon’s direction cosines. [Footnote 363-2]
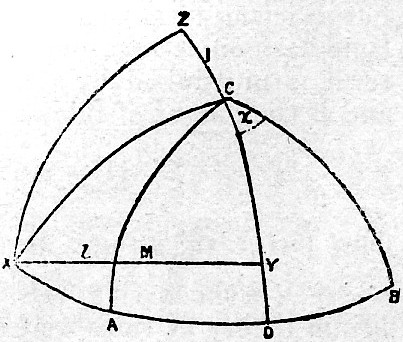
Fig. 2
Let A, B, C (fig. 2) be the axes fixed in the earth, C being the north pole and AB the equator, let X, Y, Z be a second set of axes, XY being the plane of the moon’s orbit; M the projection of the moon in her lunar orbit; I=ZC, the obliquity of the lunar orbit to the equator; χ = AX = BCY; l = MX, the moon’s longitude in her orbit measured from X, the intersection of the equator with the lunar orbit, hereafter called the "intersection." Then
These are the required functions of M1, M2, M3.
Now let c be the moon’s mean distance, e the eccentricity of the moon’s orbit, and let
Corresponding to the definition of a simple tide given § 1, the expression for each term of the tide-generating potential should consist of a solid spherical harmonic, multiplied by a simple time-harmonic. In (71) ρ2ξη, ρ2(ξ2 - η2), &c. are solid spherical harmonics, and in order to complete the expression for V it is necessary to develop the five functions of X, Y, Z in a series of simple time-harmonics. But (71) may be simplified in such a way that the five functions are reduced to three. The axes fixed in the earth may be taken, as in § 7, to have their extremities as follows:—the axis C north pole, the axis B 90° E. of A on the equator, and the axis A on the equator, and the axis A on the equator in the meridian of the place of observation. Thus, if λ be the latitude of that place, we have
ξ = cos λ, η = 0, ζ = sin λ
Then, writing a for the earth’s radius at the place of observation, (71) becomes
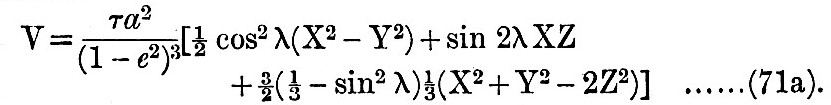
The process of developing the three functions of X, Y, Z consists in the introduction of the formulae of elliptic motion into (66) and (70), the subsequent development of the X-Y-Z functions in a series of trigonometrical terms, and the rejection of terns which appear numerically to be negligible. The terms depending on the principal lunar inequalities—evection and variation—are also introduced. Finally, the three X-Y-Z functions are obtained as a series of simple time-harmonics, with the arguments of the sines and cosines linear functions of the earth’s rotation, the moon’s mean motion, and the longitude of the moon’s perigee. The next step is to pass, according to the principle of forced oscillations, from the potential to the height of tide generated by the forces corresponding to that potential. The X-Y-Z functions being simple time-harmonics, the principle of forced vibrations allows us to conclude that the forces corresponding to V in (71a) will generate oscillations in the ocean of the same periods and types as the terms in V but of unknown amplitudes and phases. Now let 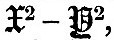 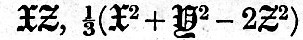 be three functions having respectively similar forms to those of be three functions having respectively similar forms to those of
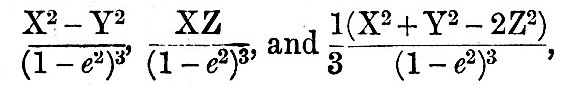
but differing from them in that the argument of each of the simple tune-harmonies has some angle subtracted from it and that the term is multiplied by a numerical factor. Then, if g be gravity and h be the height of tide at the place of observation, we must have
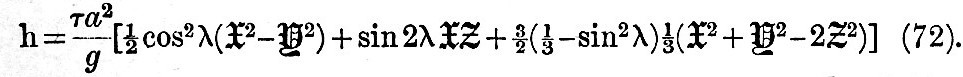
The factor τa2/g may be more conveniently written 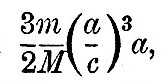 , ,
where M is the earth’s mass. It has been so chosen that, if the equilibrium theory of tides were fulfilled, with water covering the whole earth, the numerical factors in the 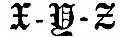 functions would be each unity and the alterations of phase would be zero. The terms in functions would be each unity and the alterations of phase would be zero. The terms in 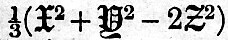 require special consideration. The function of the latitude being require special consideration. The function of the latitude being 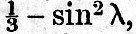 , it follows that, when in the northern hemisphere it is high water north of a certain critical latitude, it is low water on the opposite side of that parallel; and the same is true of the southern hemisphere. It is best to adopt a uniform system for the whole earth, and to regard high tide and high water as consentaneous in the equatorial belt, and of opposite meaning outside of the critical latitudes. We here conceive the function always to be written , it follows that, when in the northern hemisphere it is high water north of a certain critical latitude, it is low water on the opposite side of that parallel; and the same is true of the southern hemisphere. It is best to adopt a uniform system for the whole earth, and to regard high tide and high water as consentaneous in the equatorial belt, and of opposite meaning outside of the critical latitudes. We here conceive the function always to be written 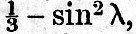 , so that outside of the critical latitudes high tide is low water. We may in continuing the development write the , so that outside of the critical latitudes high tide is low water. We may in continuing the development write the 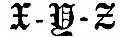 functions in the form appropriate to the equilibrium theory, with water covering the whole earth; for the actual case it is only then necessary to multiply by the reducing factor, and to subtract the phase alteration κ. As these are unknown constants for each place, they would only occur in the development as symbols of quantities to be deduced from observation. It will be understood, therefore that in the following schedules the "argument" is that part of the argument which is derived from theory, the true complete argument being the "argument" - κ, where κ is derived from observation. functions in the form appropriate to the equilibrium theory, with water covering the whole earth; for the actual case it is only then necessary to multiply by the reducing factor, and to subtract the phase alteration κ. As these are unknown constants for each place, they would only occur in the development as symbols of quantities to be deduced from observation. It will be understood, therefore that in the following schedules the "argument" is that part of the argument which is derived from theory, the true complete argument being the "argument" - κ, where κ is derived from observation.
Up to this point we have supposed the moon’s longitude and the earth’s position to be measured from the intersection; but in order to pass to the ordinary astronomical formula we must measure the longitude and the earth’s position from the vernal equinox. Hence we determine the longitude and right ascension of the intersection in terms of the longitude of the moon’s node and the inclination of the lunar orbit, and introduce them into our formulae for the 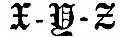 functions. The expressions for the functions corresponding to solar tides may be written down by symmetry, and in this case the intersection is actually the vernal equinox. functions. The expressions for the functions corresponding to solar tides may be written down by symmetry, and in this case the intersection is actually the vernal equinox.
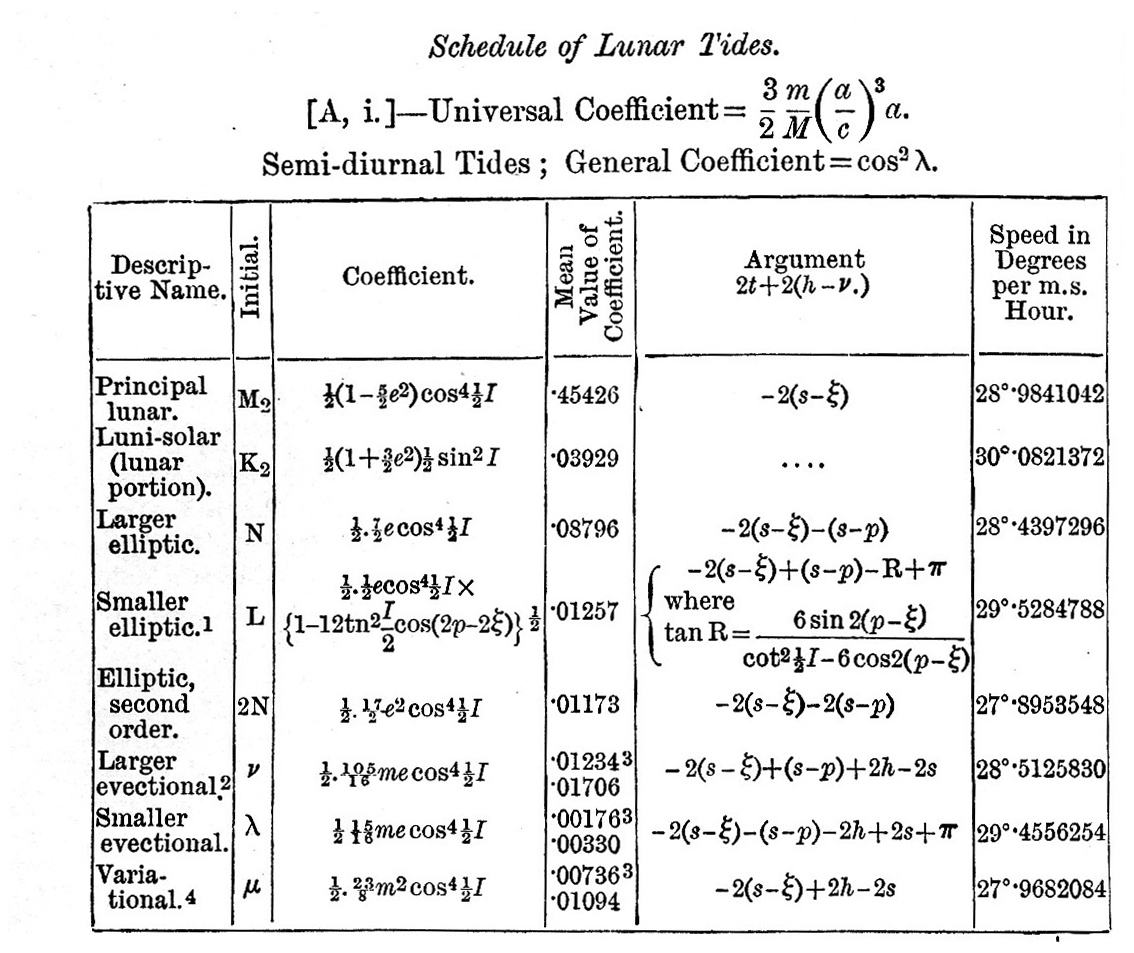
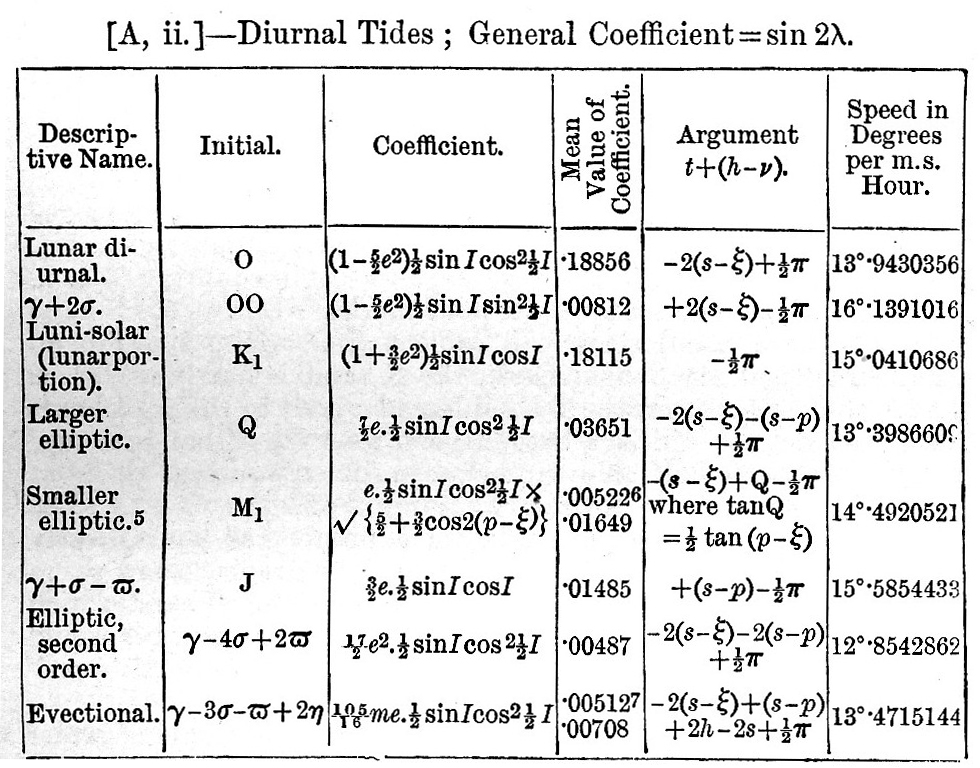
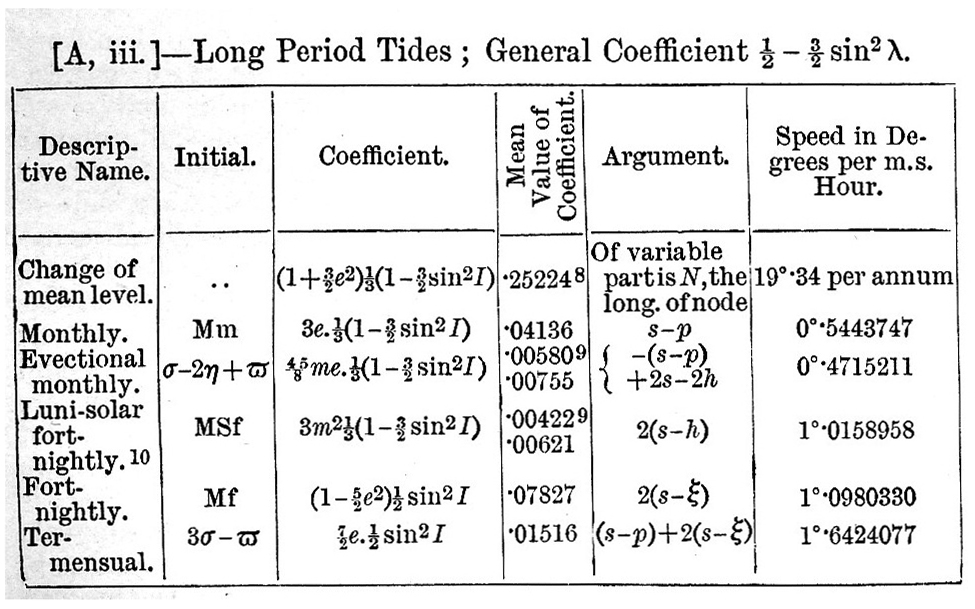
The final result of the process sketched is to obtain a series of terms each of which is a function of the elements of the moon’s or sun’s orbit and a function of the terrestrial latitude of the place of observation, multiplied by the cosine of an angle which increases uniformly with the time. We shall now write down the result in the form of a schedule; but we must first state the notation employed:— e, e = eccentricities of lunar and solar orbits; I, ω = obliquities of equator to lunar orbit and ecliptic; p, p = longitudes of lunar and solar perigees; 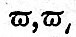 = hourly increments of p, p; s, h = moon’s and sun’s mean longitudes ; σ, η = hourly increments of s, h; t = local mean solar time reduced to angle ; γ - η = 15° per hour; λ = latitude of place of observation; ξ, ν = longitude in lunar orbit, and R.A. of the intersection; N = longitude of moon’s node; i = inclination of lunar orbit. The speed of any tide is defined as the rate of increase of its argument, and is expressible, therefore, as a linear function of = hourly increments of p, p; s, h = moon’s and sun’s mean longitudes ; σ, η = hourly increments of s, h; t = local mean solar time reduced to angle ; γ - η = 15° per hour; λ = latitude of place of observation; ξ, ν = longitude in lunar orbit, and R.A. of the intersection; N = longitude of moon’s node; i = inclination of lunar orbit. The speed of any tide is defined as the rate of increase of its argument, and is expressible, therefore, as a linear function of 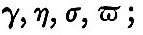 ; for we may neglect ; for we may neglect 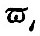 , as being very small. , as being very small.
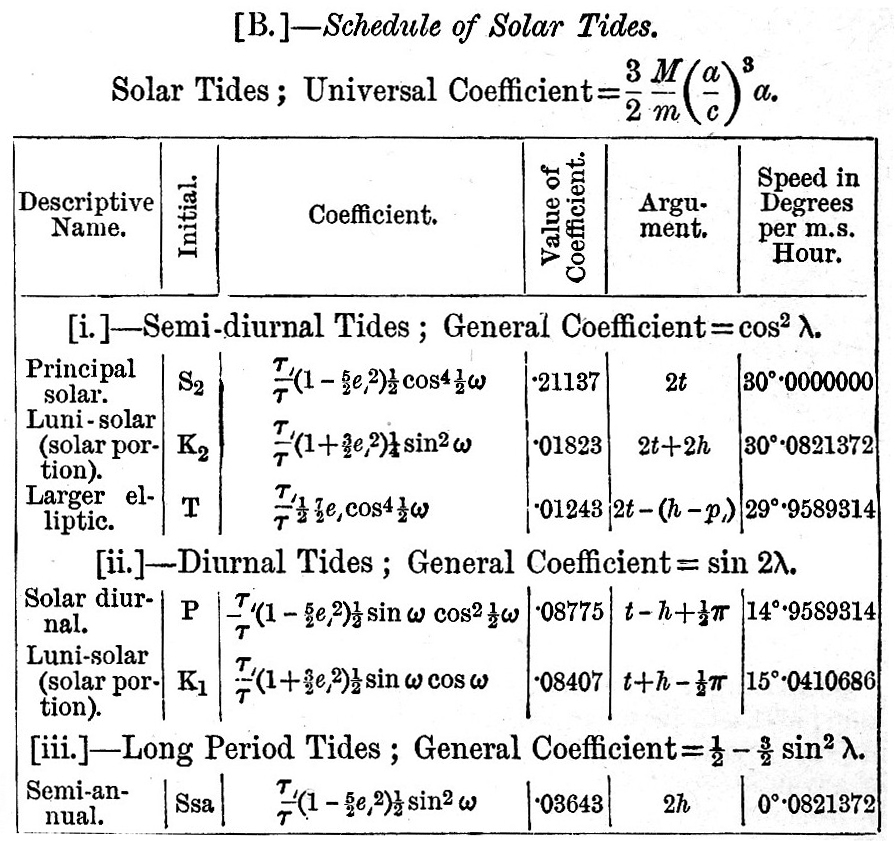
The following schedules, then, give h the height of tide. The arrangement is as follows. First, there is a universal coefficient 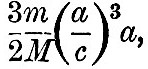 , which multiplies every term of all the schedules. Secondly, there are general coefficients, one for each schedule, viz., cos2 λ for the semi-diurnal terms, sin 2λ for the diurnal, and , which multiplies every term of all the schedules. Secondly, there are general coefficients, one for each schedule, viz., cos2 λ for the semi-diurnal terms, sin 2λ for the diurnal, and 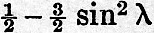 for the terms of long period. In each schedule the third column, headed "coefficient," gives the functions of I and e (and in two cases also of p). In the fourth column is given the mean semi-range of the corresponding term in numbers, which is approximately the value of the coefficient in the first column when I = ω but we pass over the explanation of the mode of computing the values. The fifth column contains arguments linear functions of t, h, s, p, v, ξ. In [A, i.] 2t + 2(h - v) and in [A, ii.] t + (h - v) are common to all the arguments. The arguments are grouped in a manner convenient for subsequent computation. Lastly, the sixth is a column of speeds being the hourly increase of the arguments in the preceding column, estimated in degrees per hour. It has been found practically convenient to denote each of these partial tides by an initial letter, arbitrarily chosen In the first column we give a descriptive name for the tide, and in the second the arbitrarily chosen initial. In some cases no initial has been chosen, and here we indicate the tide by the analytical expression for its speed, or hourly increase of argument. for the terms of long period. In each schedule the third column, headed "coefficient," gives the functions of I and e (and in two cases also of p). In the fourth column is given the mean semi-range of the corresponding term in numbers, which is approximately the value of the coefficient in the first column when I = ω but we pass over the explanation of the mode of computing the values. The fifth column contains arguments linear functions of t, h, s, p, v, ξ. In [A, i.] 2t + 2(h - v) and in [A, ii.] t + (h - v) are common to all the arguments. The arguments are grouped in a manner convenient for subsequent computation. Lastly, the sixth is a column of speeds being the hourly increase of the arguments in the preceding column, estimated in degrees per hour. It has been found practically convenient to denote each of these partial tides by an initial letter, arbitrarily chosen In the first column we give a descriptive name for the tide, and in the second the arbitrarily chosen initial. In some cases no initial has been chosen, and here we indicate the tide by the analytical expression for its speed, or hourly increase of argument.
The schedule for the solar tides is drawn up in precisely the same manner, the only difference being that the coefficients are absolute constants. The eccentricity of the solar orbit is so small that the elliptic tides may be omitted, except the larger elliptic semi-diurnal tide. In order that the comparison of the importance of the solar tides with the lunar may be complete, the same universal coefficient 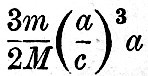 is retained, and the special coefficients for each term is made to involve the factor is retained, and the special coefficients for each term is made to involve the factor 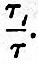 . Here . Here 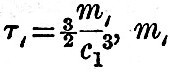 being the sun’s mass. With being the sun’s mass. With
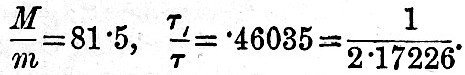
To write down any term take the universal coefficient, the general coefficient for the class of tides, the special coefficient, and multiply by the cosine of the argument. The result, taken with the positive sign, is a term in the equilibrium tide, with water, covering the whole earth. The transition to the actual case by the introduction of a factor and a delay of phase (to be derived from observation) has been already explained. The sum of all the terms is the complete expression for the height of tide h.
From the fourth columns we see that the coefficients in descending order of magnitude are M2, K1 (both combined), S2, O, K1 (lunar), N, P, K1 (solar), K2 (both combined), K2 (lunar), Mf, Q, Mm, K2 (solar), Ssa, v , M1, J, L, T, 2N, μ, OO, 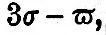 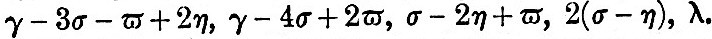 . .
The tides depending on the fourth power of the moon’s parallax arise from the potential 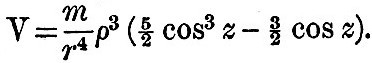 They give rise to a small diurnal tide M1, and to a small ter-diurnal tide M3; but we shall not give the analytical development. They give rise to a small diurnal tide M1, and to a small ter-diurnal tide M3; but we shall not give the analytical development.
Footnotes
(a) referring to the text section above
363-2 For further details of the analysis of this section, see the Report "On Harmonic Analysis, &c.," for 1883 to the British Association (Southport).
(b) referring to the tables above
(1) Fused with 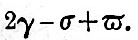 . .
(2) m is the ratio of the moon’s mean motion to the sun’s.
(3) In these entries the lower number gives the value when the co-efficients of the evection and variation have their full values as derived from lunar theory.
(4) Indicated by 2MS as a compound tide (see below, § 24).
(5)
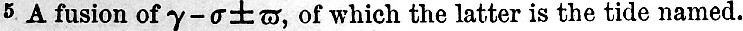
(6)
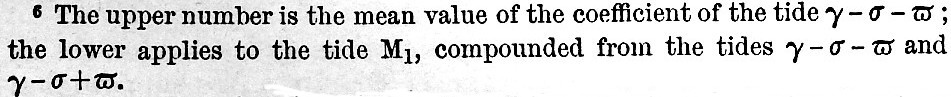
(7) The lower number gives the value when the coefficients in the evection have their full value as derived from lunar theory.
(8)

(9) The lower of these two numbers gives the value when the coefficients in the evection and variation have their full values as derived from lunar theory.
(10) Indicated by MSf as a compound tide.
Read the rest of this article:
Tides - Table of Contents
|