1902 Encyclopedia > Tides > [Harmonic Analysis] On the Form of Presentation of Results of Tidal Observation
Tides
(Part 25)
IV. HARMONIC ANALYSIS (cont.)
25. On the Form of Presentation of Results of Tidal Observation
Supposing n to be the speed of any tide in degrees per mean solar hour, and t to be mean solar time elapsing since Oh of the first day of (say) a year of continuous observation, then the immediate result of harmonic analysis is to obtain A and B, two heights (estimated in feet and tenths) such that the height of this tide at the time t is given by A cos nt + B sin nt. If we put 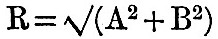 and tan ζ = B/A, then the tide is represented by and tan ζ = B/A, then the tide is represented by
In this form R is the semi-range of the tide in British feet, and ζ is an angle such that ζ/n is the time elapsing after 0h of the first day until it is high water of this particular tide. It is obvious that ζ may have any value from 0° to 360°, and that the results of the analysis of successive years of observation will not be comparable with one another when presented in this form.
But let us suppose that the results of the analysis are presented in a number of terms of the form
where V is a linear function of the moon’s and sun’s mean longitudes, the mean longitude of the moon’s and sun’s perigees, and the local mean solar time at the place of observation, reduced to angle at 15° per hour. V increases uniformly with the time, and its rate of increase per mean solar hour is the n of the first method, and is called the speed of the tide. It is supposed that u stands for a certain function of the longitude of the node of the lunar orbit at an epoch half a year later than Oh of the first day. Strictly speaking, u should be taken as the same function of the longitude of the moon’s node, varying as the node moves; but, as the variation is but small in the course of a year, u may be treated as a constant and put equal to an average value for the year, which average value is taken as the true value of u at exactly mid year. Together V + u constitute that function which has been tabulated as the "argument" in the schedules of § 23. Since V + u are together the whole argument according to the equilibrium theory of tides, with sea covering the whole earth, it follows that κ/n is the lagging of the tide which arises from kinetic action, friction of the water, imperfect elasticity of the earth, and the distribution of land. It is supposed that H is the mean value in British feet of the semi-range of the particular tide in question; f is a numerical factor of augmentation or diminution, due to the variability of the obliquity of the lunar orbit. The value of f is the ratio of the "coefficient" in the third column of the preceding schedules to the mean value of the same term. For example, for all the solar tides f is unity, and for the principal lunar tide M2 it is equal to 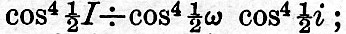 for the mean value of this term has a coefficient for the mean value of this term has a coefficient 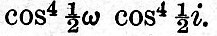 It is obvious, then, that, if the tidal observations are consistent from year to year, H and κ should come out the same from each year’s reductions. It is only when the results are presented in such a form as this that it will be possible to judge whether the harmonic analysis is yielding satisfactory results. This mode of giving the tidal results is also essential for the use of a tide-predicting machine (see § 38). It is obvious, then, that, if the tidal observations are consistent from year to year, H and κ should come out the same from each year’s reductions. It is only when the results are presented in such a form as this that it will be possible to judge whether the harmonic analysis is yielding satisfactory results. This mode of giving the tidal results is also essential for the use of a tide-predicting machine (see § 38).
We must now show how to determine H and κ from R and ζ. It is clear that H = H/f, and the determination of f from the schedules depends on the evaluation of the mean value of each of the terms in the schedules, into which we shall not enter. If V0 be the value of V at 0h of the first day, then clearly
Thus the rule for the determination of κ is: Add to the value of ζ the value of the argument at 0h of the first day.
The results of harmonic analysis are usually tabulated by giving H, κ under the initial letter of each tide; the results are thus comparable from year to year. [Footnote 366-1] For the purpose of using the tide-predicting machine the process of determining H and κ from R and ζ has simply to be reversed, with the difference that the instant of time to which to refer the argument is 0h of the first day of the new year, and we must take note of the different value of u and f for the new year. Tables [Footnote 366-2] have been computed for f and u for all longitudes of the moon’s node and for each kind of tide, and the mean longitudes of moon, sun, and lunar perigee may be extracted from any ephemeris. Thus when the mean semi-range H and retardation κ of any tide are known its height may be computed for any instant. The sum of the heights for all the principal tides of course gives the actual height of water.
Footnotes
366-1 See, for example, a collection of results by Baird and Darwin, Proc. Roy. Soc., No. 239, 1885.
366-2 Report on Harmonic Analysis to Brit. Assoc., 1883, and more extended table in Baird's Manual of Tidal Observation, London, 1887.
Read the rest of this article:
Tides - Table of Contents
|