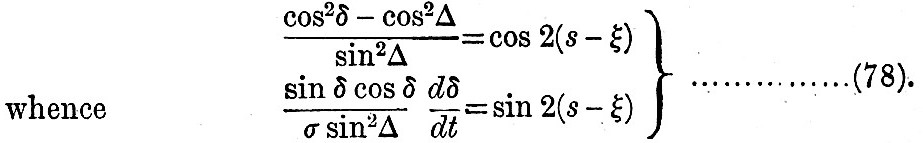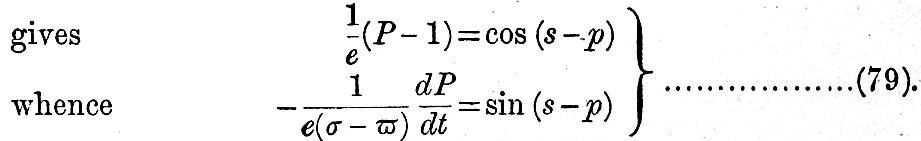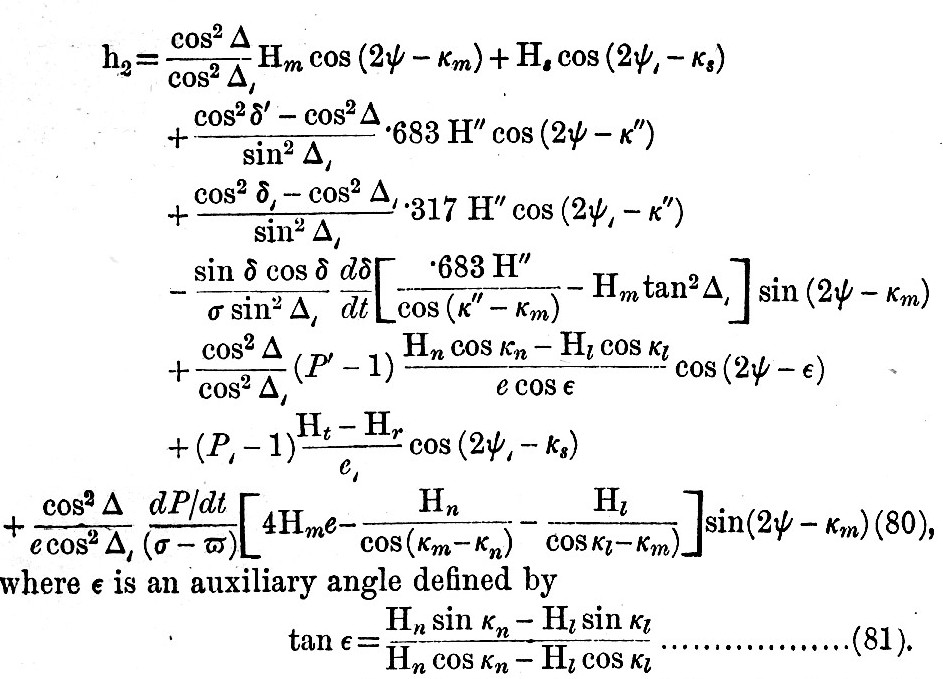1902 Encyclopedia > Tides > [Synthetic Method] Semi-Diurnal Tides
Tides
(Part 29)
V. SYNTHETIC METHOD (cont.)
29. Semi-Diurnal Tides
The process adopted is to replace the mean longitudes and elements of the orbit in each term of the harmonic development of the schedules of § 23 by hour-angles, declinations, and parallaxes.
At the time t (mean solar time of port reduced to angle) let α, δ, ψ 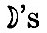 R.A., declination, and hour-angle, and l R.A., declination, and hour-angle, and l 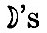 longitude measured from the "intersection." These and other symbols when written with subscript accent are to apply to the sun. Then ν being the R.A. of the intersection, we have from the right-angled spherical triangle of which the sides are l, δ, α - ν the relations longitude measured from the "intersection." These and other symbols when written with subscript accent are to apply to the sun. Then ν being the R.A. of the intersection, we have from the right-angled spherical triangle of which the sides are l, δ, α - ν the relations
Now s - ξ is the 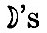 mean longitude measured from the intersection and s - p is the mean anomaly; hence approximately mean longitude measured from the intersection and s - p is the mean anomaly; hence approximately
From (74) and (75) we have approximately
Now, h being the 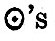 mean longitude, t + h is the sidereal hour-angle, and mean longitude, t + h is the sidereal hour-angle, and
we have approximately from (74) and (75)
Obviously Δ is such a declination that sin2 Δ is the mean value of sin2 δ during a lunar month. Again, if P be the ratio of the 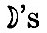 parallax to her mean parallax, the equation to the ellipse described parallax to her mean parallax, the equation to the ellipse described
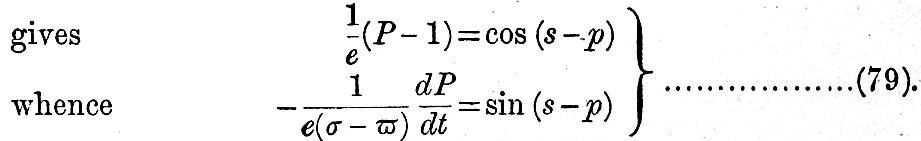
Now it appears in schedule A of § 23 that the arguments of all the lunar semi-diurnal tides are of the form 2(t + h - ν)±2(s - ξ) or ±(s - p). It is clear, therefore, that the cosines of such angles may by the relations (76), (78), (79) be expressed in terms of hour-angles, declinations, and parallaxes. Also by means of (77) we may introduce Δ in place of I in the coefficients of each term. An approximate formula for Δ is 16°.51 + 3°.44 cos N - 0°.19 cos 2N. In the Report to the British Association for 1885, the details of the processes indicated are given.
Before giving the formula it must be remarked that the result is expressed more succinctly by the introduction of the symbol δ″ to denote the 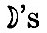 declination at a time earlier than that of observation by an interval which may be called the "age of the declinational inequality," and is computed from the formula tan (κ″ - κm /2σ or 52h.2 tan (κ″ - κm). Similarly, it is convenient to introduce P′ to denote the value of P at a time earlier than that of observation by the "age of the parallactic inequality," to be computed from declination at a time earlier than that of observation by an interval which may be called the "age of the declinational inequality," and is computed from the formula tan (κ″ - κm /2σ or 52h.2 tan (κ″ - κm). Similarly, it is convenient to introduce P′ to denote the value of P at a time earlier than that of observation by the "age of the parallactic inequality," to be computed from 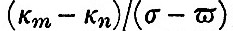 or 105h.3 tan (κm - κn). These two "ages" probably do not differ in general much from a third period, computed from (κ8 - κm)/2/(σ - η), which is called the "age of the tide." or 105h.3 tan (κm - κn). These two "ages" probably do not differ in general much from a third period, computed from (κ8 - κm)/2/(σ - η), which is called the "age of the tide."
The similar series of transformations when applied to the solar tides to simpler results, because 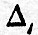 is a constant, being 16°·33, and the "ages" may be treated as zero; besides the terms depending on is a constant, being 16°·33, and the "ages" may be treated as zero; besides the terms depending on 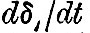 and and 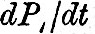 are negligible. If now we denote by h2 the height of water with reference to mean watermark, in so far as the height is affected by the harmonic tides M2, S2, K2, N, L, T, R, [Footnote 367-1] the harmonic expression is transformed into are negligible. If now we denote by h2 the height of water with reference to mean watermark, in so far as the height is affected by the harmonic tides M2, S2, K2, N, L, T, R, [Footnote 367-1] the harmonic expression is transformed into
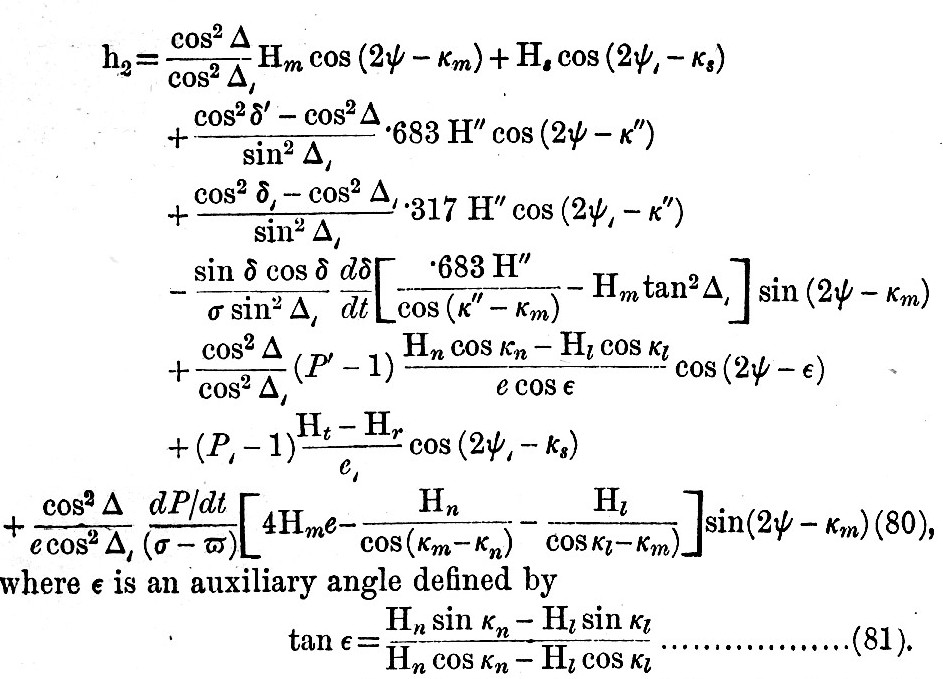
The first two terms are the principal tides, and the physical origin of the remaining small terms is indicated by their involving 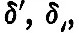 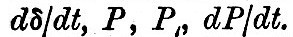 The terms in dδ/dt and dP/dt are generally smaller than the others. The terms in dδ/dt and dP/dt are generally smaller than the others.
The approximation may easily be carried further. But the above is in some respects a closer approximation than the expression from which it is derived, since the hour-angles, declinations, and parallaxes necessarily involve all the lunar and solar inequalities.
Footnote
367-1 R is the smaller solar elliptic tide bearing the same relation to T that L does to N amongst the lunar tides. It was omitted as unimportant in schedule [B.i.] of § 23.
Read the rest of this article:
Tides - Table of Contents
|