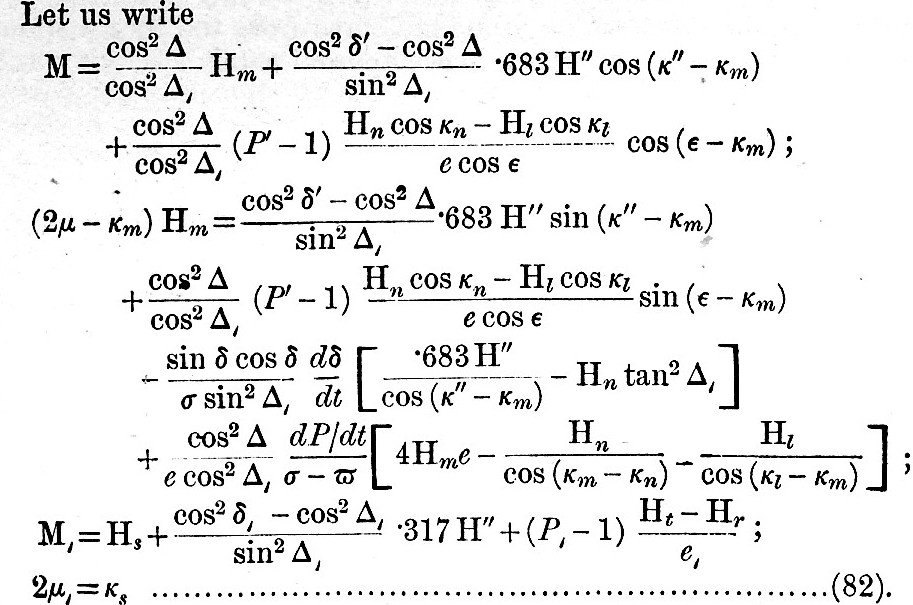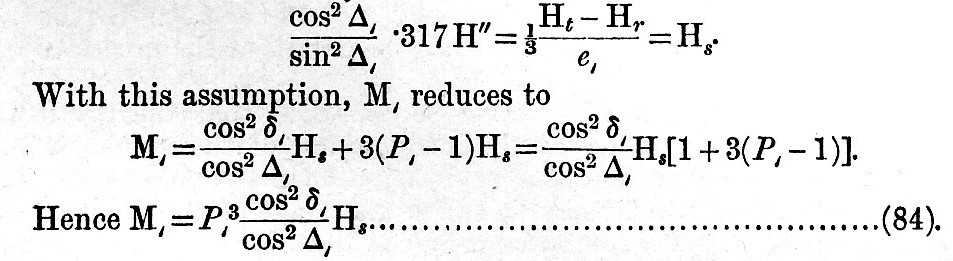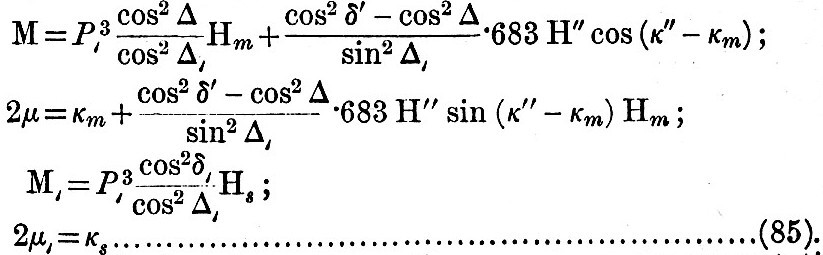V. SYNTHETIC METHOD (cont.)
30. Synthesis of Solar and of Lunar Portions of the Semi-Diurnal Tide
Since observation and theory agree in showing that κ″ is generally very nearly equal to κ8, we are justified in substituting &kappa8 for κ″ in small solar declinational term of (80) involving ·317 H″. Then, using (82) in (80),
If the equilibrium theory of tides were true, each H would be proportional to the corresponding term in the harmonically developed potential. This proportionality holds nearly between tides of almost the same speed; hence, using the expressions in the column of coefficients in schedule [B, i. ], § 23 (with the additional tide R there omitted, but having a coefficient 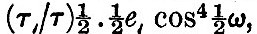 , found by symmetry with the lunar tide L), and introducing Δ in place of ω in the solar tides, we may assume the truth of the proportion
, found by symmetry with the lunar tide L), and introducing Δ in place of ω in the solar tides, we may assume the truth of the proportion
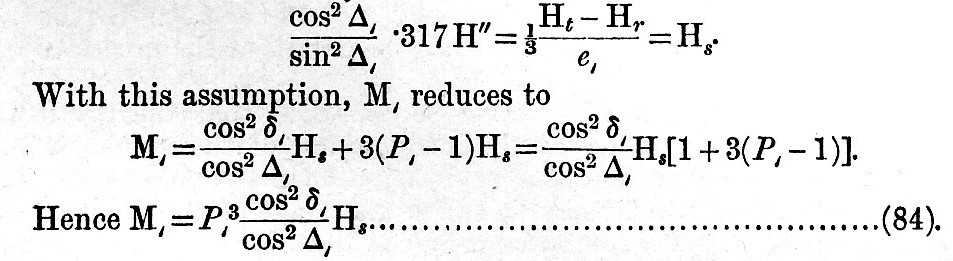
This is the law which we should have derived directly from the equilibrium theory, with the hypothesis that all solar semi-diurnal tides suffer nearly equal retardation. Save for meteorological influences, this must certainly be true.
A similar synthesis of M cannot be carried out, because the considerable diversity of speed amongst the lunar tides makes a similar appeal to the equilibrium theory incorrect. It may be seen, however, that it would be more correct to write cos2 δ′ instead of cos2 Δ′ in the coefficient of the parallactic terms in M and 2μ.
The three terms of M in (82) give the height of lunar tide with its declinational and parallactic corrections, and similarly the formula for μ in (82) gives its value and corrections.
If now τ denotes the mean solar time elapsing since the moon's upper transit and γ the angular velocity of the earth’s rotation, it is clear that the moon’s hour-angle
and, since M cos 2(ψ - μ) is a maximum when ψ = μ or differs from μ by 180°, it follows that μ/(γ - dα/dt) is the "interval" from the moon’s upper or lower transit to high water of the lunar tide. Since τ is necessarily less than 12h, we may during the interval from transit to high water take as an approximation dα/dt = σ, the moon’s mean motion.[Footnote 368-1] Hence that interval is μ/(γ - σ), or 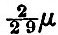 hours nearly, when μ is expressed in degrees. Thus (82) for μ gives by its first term the mean interval for the lunar tide, and by the subsequent terms the declinational and parallactic corrections.
hours nearly, when μ is expressed in degrees. Thus (82) for μ gives by its first term the mean interval for the lunar tide, and by the subsequent terms the declinational and parallactic corrections.
We have said that the synthesis of M cannot be carried out as in the case of 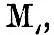 but the partial synthesis below will give fairly good results. The proposed formula is
but the partial synthesis below will give fairly good results. The proposed formula is
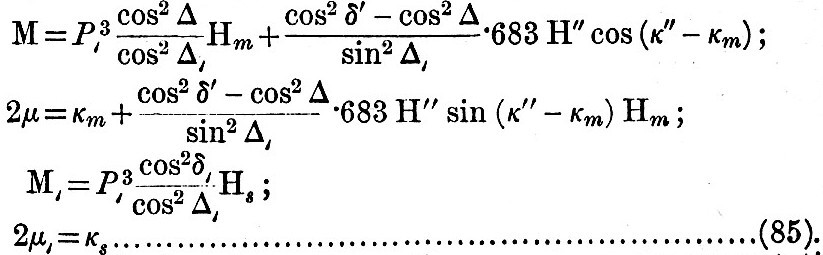
These formulae have been used in the example of the computation of a tide-table given in the Admiralty Scientific Manual (1886).
Footnote
368-1 The tide has been referred by Lubbock and others to an earlier transit, and not to the one immediately preceding the time under consideration. In this case we cannot admit with great accuracy that dα/dt = σ, since the interval may be 30 or 40 hours.
Read the rest of this article:
Tides - Table of Contents