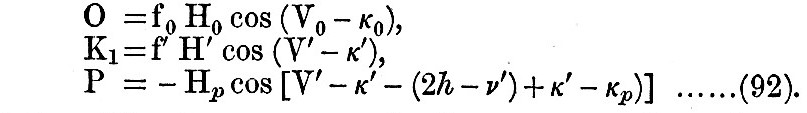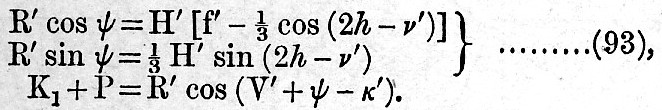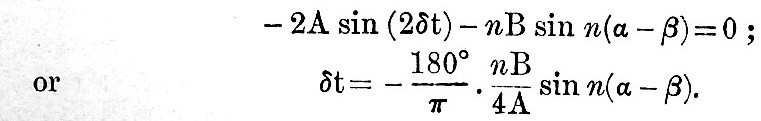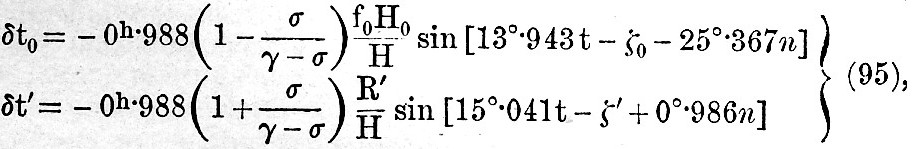1902 Encyclopedia > Tides > [Synthetic Method] Diurnal Tides
Tides
(Part 32)
V. SYNTHETIC METHOD (cont.)
32. Diurnal Tides
These tides have not been usually treated with completeness in the synthetic method. In the tide-tables of the British Admiralty we find that the tides at some ports are "affected by diurnal inequality"; such a statement may be interpreted as meaning that the tides are not to be predicted by the information given in the so-called tide-table. The diurnal tides are indeed complex, and do not lend themselves easily to a complete synthesis. In the harmonic notation the three important tides are K1, O, P, and the lunar portion of K1 is nearly equal to O in height, whilst the solar portion is nearly equal to P. A complete synthesis may be carried out on the lines adopted in treating the semi-diurnal tides, but the advantage of the plan is lost in consequence of large oscillations of the amplitude through the value zero, so that the tide is often represented by a negative quantity multiplied by a circular function. It is best, then, only to attempt a partial synthesis, and to admit the existence of two diurnal tides.
We see from schedules [A, ii.] and [B, i.], § 23, that the principal diurnal tides are those lettered O, P, K1. Of these K1 occurs both for the moon and the sun. The synthesis of the two parts of K1 is effected without difficulty, and the result is a formula for the total K1 tide like that in [A, ii.], but with the ν which occurs in the argument replaced by a different angle denoted as ν′. If, then, we write
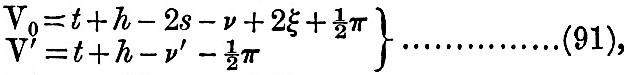
the three tides O, K1, P are written as follows :—
The last two tides have very nearly the same speed, so that we may assume κ′ = κp, and that Hp has the same ratio to H′ as in the equilibrium theory. Now, in schedules [A, ii.], [B, ii.], § 23, the coefficient of K1, viz., H″ (the sum of the lunar and solar parts), is ·26522, and the coefficient of P, viz., Hp, is ·08775, so that H″ = 3·023 Hp, or say = 3Hp, Hence we have
It is clear that φ and R′ have a semi-annual inequality, and therefore for several weeks together R′ and φ may be treated as constant.
Now suppose that we compute V0 and V′ at the epoch—that is, at the initial noon of the period during which we wish to predict the tides—and with these values put
Then the speed of V0, is γ - 2σ, or 13º·94303 per hour, or 360º — 25º·3673 per day; and the speed of V′ is γ, or 15º·0410686 per hour, or 360º·9856 per day. Hence, if t be the mean solar time on the (n + 1)th day since the initial moment or epoch,
Therefore the diurnal tides at time t of the (n + l)th day are given by
If we substitute for t the time of high or low water as computed simply from the semi-diurnal tide, it is clear that the sum of these two expressions will give the diurnal correction for height of tide at high or low water, provided the diurnal tides are not very large. If we consider the maximum of a function
where B is small compared with A and n is nearly unity, we see that the tine of maximum is given approximately by t = α, with a correction δt determined from
In this way we find that the corrections to the time of high water from O and K1 + P are
H denoting the height and t the time of high water as computed from the semi-diurnal tide. If t next denotes the time of low water the same corrections with opposite sign give the corrections for low water.
If the diurnal tides are large a second approximation will be necessary. These formulae have been used in computing a tide-table in the example given in the Admiralty Scientific Manual (1886).
Read the rest of this article:
Tides - Table of Contents
|