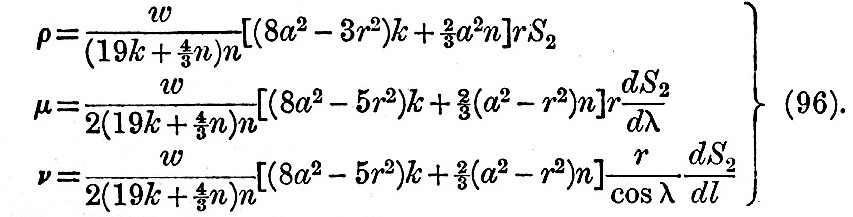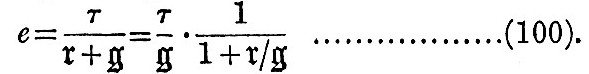1902 Encyclopedia > Tides > [Tidal Deformation of the Solid Earth] Elastic Tides
Tides
(Part 43)
VIII. TIDAL DEFORMATION OF THE SOLID EARTH
43. Elastic Tides
The tide-generating potential varies as the square of the distance from the earth’s centre, and the corresponding forces act at every point throughout its mass. No solid matter possesses the property of absolute rigidity, and we must therefore admit the probable existence of tidal elastic deformation of the solid earth. The problem of finding the state of strain of an elastic sphere under given stresses was first solved by Lamé; [Footnote 373-1] he made, however, but few physical deductions from his solution. An independent solution was found by Sir W. Thomson, [Footnote 373-2] who drew some interesting conclusions concerning the earth.
His problem, in as far as it is now material, is as follows. Let a sphere, of radius a and density w, be made of elastic material whose bulk and rigidity moduli are k and n, and let it be subjected to forces due to a potential wr2S2 per unit volume, where S2 is a surface spherical harmonic of the second order. Then it is required to find the strain of the sphere. We refer the reader to the original sources for the methods of solution applicable to spherical shells and to solid spheres. In order to write Thomson’s solution we put r, λ ,l for radius vector, latitude, and longitude, and ρ, μ, ν for the corresponding displacements. Then the solution is as follows:--
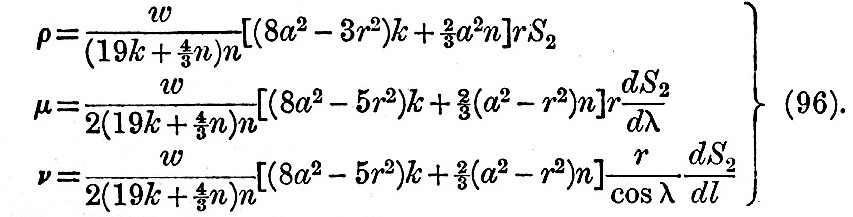
For either tidal or rotational stresses
in the case of tides 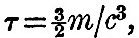 m and c being the moon’s mass and distance, and in the case of rotation m and c being the moon’s mass and distance, and in the case of rotation 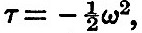 being the angular velocity about the polar axis. The equation to the surface is found by putting r = a + ρ, where in the expression for ρ we put r = a. Hence from (96) the form of surface is given by being the angular velocity about the polar axis. The equation to the surface is found by putting r = a + ρ, where in the expression for ρ we put r = a. Hence from (96) the form of surface is given by
In most solids the bulk modulus is considerably larger than the rigidity modulus, and in this discussion it is sufficient to neglect n compared with k. With this approximation, the ellipticity e of the surface becomes
Now suppose the sphere to be endued with the power of gravitation, and write
where g is gravity at the surface of the globe. Then, if there were no elasticity, the ellipticity would be given by 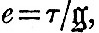 , and without gravitation by , and without gravitation by 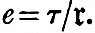 And it may be proved in several ways that, gravity and elasticity co-operating, And it may be proved in several ways that, gravity and elasticity co-operating,
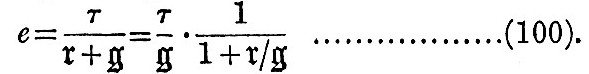
If n be the rigidity of steel, and if the globe have the size and mean density of the earth, 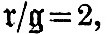 and with the rigidity of glass and with the rigidity of glass 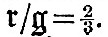 Hence the ellipticity of an earth of steel under tide-generating force would be Hence the ellipticity of an earth of steel under tide-generating force would be 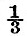 of that of a fluid earth, and the similar fraction for glass would be of that of a fluid earth, and the similar fraction for glass would be 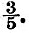 If an ocean be superposed on the globe, then, if the globe rises and falls with the tide as though it were fluid, there will obviously be no tide visible to an observer carried up and down with the solid; and with any degree of rigidity the visible tide will be the excess of the fluid tide above the solid tide. Hence on an earth with rigidity of steel the oceanic tides would be reduced to If an ocean be superposed on the globe, then, if the globe rises and falls with the tide as though it were fluid, there will obviously be no tide visible to an observer carried up and down with the solid; and with any degree of rigidity the visible tide will be the excess of the fluid tide above the solid tide. Hence on an earth with rigidity of steel the oceanic tides would be reduced to 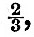 and with rigidity of glass to and with rigidity of glass to 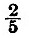 of the tides on a rigid earth. of the tides on a rigid earth.
Footnotes
373-1 Théorie Math. de l’Élasticité, 1866, p. 213.
373-2 Thomson and Tait, Nat. Phil., §§ 732-737 and 833-842, or Phil. Trans., pt. ii., 1863, p. 583.
Read the rest of this article:
Tides - Table of Contents
|