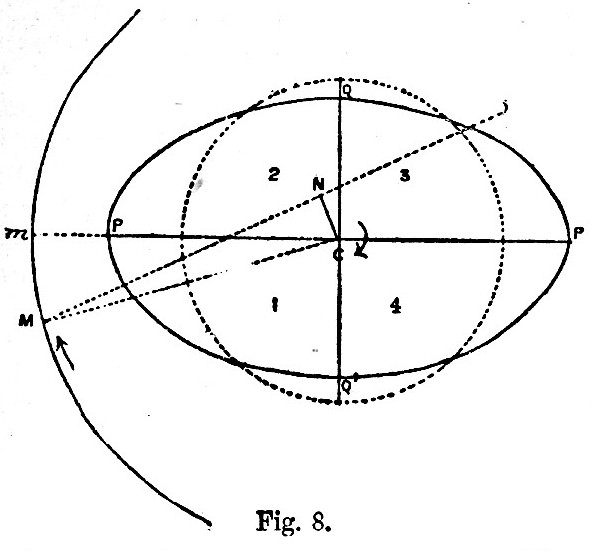
In fig. 8 the paper is supposed to be the plane of the orbit of a satellite M revolving in the direction of the arrow about the planet C, which rotates in the direction of the arrow about an axis perpendicular to the paper. The rotation of the planet is supposed to be more rapid than that of the satellite, so that the day is shorter than the month. Let us suppose that the planet is either entirely fluid, or has an ocean of such depth that it is high water under or nearly under the satellite. When there is no friction, with the satellite at m, the planet is elongated into the ellipsoidal shape shown, cutting the mean sphere, which is dotted. But, when there is friction in the fluid motion, the tide is retarded, and high tide occurs after the satellite has passed the meridian. Then, if we keep the same figure to represent the tidal elongation, the satellite must be at M, instead of at m. If we number the four quadrants as shown, the satellite must be in quadrant 1. The protuberance P is nearer to the satellite than P', and the deficiency Q is further away than the deficiency Q″. Hence the resultant action of the planet on the satellite must be in some such direction as MN. The action of the satellite on the planet is equal and opposite, and the force in NM, not being through the planet’s centre, must produce a retarding couple on the planet’s rotation, the magnitude of which depends on the length of the arm CN. This tidal frictional couple varies as the height of the tide, and also depends on the satellite’s distance; its intensity in fact varies as the square of the tide-generating force, and therefore as the inverse sixth power of the satellite’s distance. Thus tidal friction must retard the planetary rotation. Let us now consider its effect on the satellite. If the force acting on M be resolved along and perpendicular to the direction CM, the perpendicular component tends to accelerate the satellite’s velocity. It alone would carry the satellite further from C than it would be dragged back by the central force towards C. The satellite would describe a spiral, the coils of which would be very nearly circular and very nearly coincident. If now we resolve the central component force along CM tangentially and perpendicular to the spiral, the tangential component tends to retard the velocity of the satellite, whereas the disturbing force, already considered, tends to accelerate it. With the gravitational law of force between the two bodies the retardation must prevail over the acceleration. [Footnote 375-1] The moment of momentum of the whole system remains unchanged, and that of the planetary rotation diminishes, so that the orbital moment of momentum must increase; now orbital moment of momentum increases with increasing distance and diminishing linear and angular velocity of the satellite. The action of tidal friction may appear somewhat paradoxical, but it is the exact converse of the acceleration of the linear and angular velocity and the diminution of distance of a satellite moving through a resisting medium. The latter result is generally more familiar than the action of tidal friction, and it may help the reader to realize the result in the present case. Tidal friction then diminishes planetary rotation, increases the satellite’s distance, and diminishes the orbital angular velocity. The comparative rate of diminution of the two angular velocities is generally very different. If the satellite be close to the planet the rate of increase of the satellite’s periodic time or month is large compared with the rate of increase of the period of planetary rotation or day; but if the satellite is far off the converse is true. Hence, if the satellite starts very near the planet, with the month a little longer than the day, as the satellite recedes the month soon increases, so that it contains many days. The number of days in the month attains a maximum and then diminishes. Finally the two angular velocities subside to a second identity, the day and month being identical and both very long.
We have supposed that the ocean is of such depth that the tides are direct; if, however, they are inverted, with low water under or nearly under the satellite, friction, instead of retarding, accelerates the tide; and it would be easy by drawing another figure to see that the whole of the above conclusions hold equally true with inverted tides.
Footnote
375-1 This way of presenting the action of tidal friction is due to Professor Stokes.
Read the rest of this article:
Tides - Table of Contents