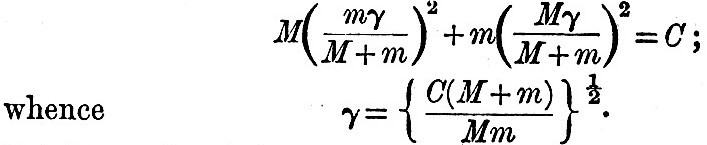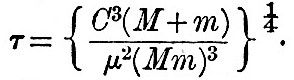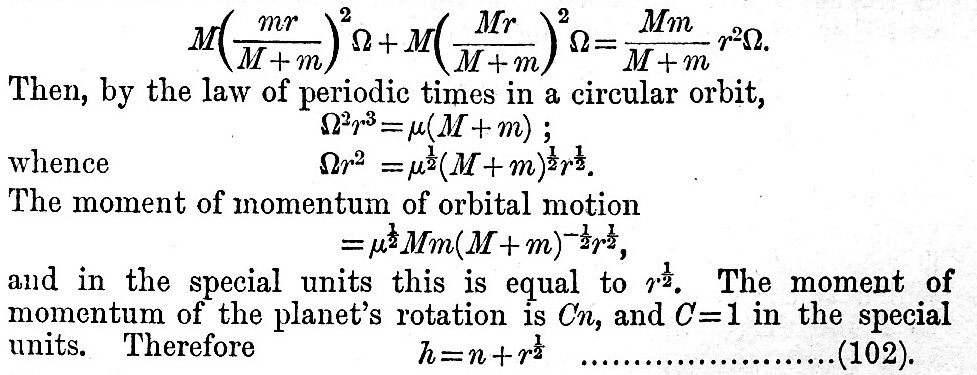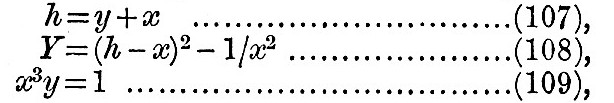1902 Encyclopedia > Tides > [Tidal Friction] Exact Investigation of the Secular Effects of Tidal Friction
Tides
(Part 47)
IX. TIDAL FRICTION (cont.)
47. Exact Investigation of the Secular Effects of Tidal Friction
The general conclusions of the last section are of such wide interest that we proceed to a rigorous discussion of the principal effects of tidal friction in the elementary case of the circular orbit. In order, however, to abridge the investigation we shall only consider the case when the planetary rotation is more rapid than the satellite’s orbital motion.
Suppose an attractive particle or satellite of mass m to be moving in a circular orbit, with an angular velocity Ω, round a planet of mass M, and suppose the planet to be rotating about an axis perpendicular to the plane of the orbit, with an angular velocity n; suppose, also, the mass of the planet to be partially or wholly imperfectly elastic or viscous, or that there are oceans on the surface of the planet; then the attraction of the satellite must produce a relative motion in the parts of the planet, and that motion must be subject to friction, or, in other words, there must be frictional tides of some sort, or other. The system must accordingly be losing energy by friction, and its configuration must change in such a way that its whole energy diminishes. Such a system does not differ much from those of actual planets and satellites, and, therefore, the results deduced in this hypothetical case must agree pretty closely with the actual course of evolution, provided that time enough has been and will be given for such changes. Let C be the moment of inertia of the planet about its axis of rotation, r the distance of the satellite from the centre of the planet, h the resultant moment of momentum of the whole system, e the whole energy, both kinetic and potential, of the system. It is assumed that the figure of the planet and the distribution of its internal density are such that the attraction of the satellite causes no couple about any axis perpendicular to that of rotation. A special system of units of mass, length, and time will now be adopted such that the analytical results are reduced to their simplest forms. Let the unit of mass be Mm/(M+m). Let the unit of length γ be such a distance that the moment of inertia of the planet about its axis of rotation may be equal to the moment of inertia of the planet and satellite, treated as particles, about their centre of inertia, when distant γ apart from one another. This condition gives
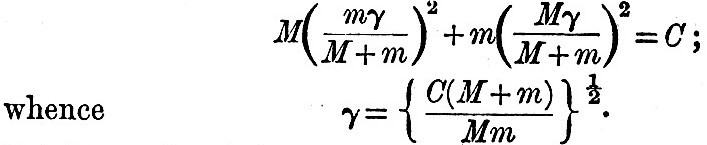
Let the unit of time τ be the time in which the satellite revolves through 57°·3 about the planet, when the satellite’s radius vector is equal to γ. In this case 1/τ is the satellite’s orbital angular velocity, and by the law of periodic times we have
where μ is the attraction between unit masses at unit distance. Then by substitution for γ
This system of units will be found to make the three following functions each equal to unity, viz., 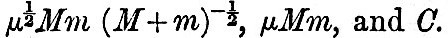 The units are in fact derived from the consideration that these functions are each to be unity. In the case of the earth and moon, if we take the moon’s mass as The units are in fact derived from the consideration that these functions are each to be unity. In the case of the earth and moon, if we take the moon’s mass as 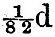 of the earth’s and the earth’s moment of inertia as of the earth’s and the earth’s moment of inertia as 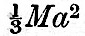 (as is very nearly the case), it may easily be shown that the unit of mass is (as is very nearly the case), it may easily be shown that the unit of mass is 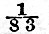 of the earth’s mass, the unit of length 5·26 earth’s radii or 33,506 kilomètres (20,807 miles), and the unit of time 2 hrs. 41 minutes. In these units the present angular velocity of the earth’s diurnal rotation is expressed by ·7044, and the moon’s present radius vector by 11·454. The two bodies being supposed to revolve in circles about their common of centre of inertia with an angular velocity Ω, the moment of momentum of orbital motion is of the earth’s mass, the unit of length 5·26 earth’s radii or 33,506 kilomètres (20,807 miles), and the unit of time 2 hrs. 41 minutes. In these units the present angular velocity of the earth’s diurnal rotation is expressed by ·7044, and the moon’s present radius vector by 11·454. The two bodies being supposed to revolve in circles about their common of centre of inertia with an angular velocity Ω, the moment of momentum of orbital motion is
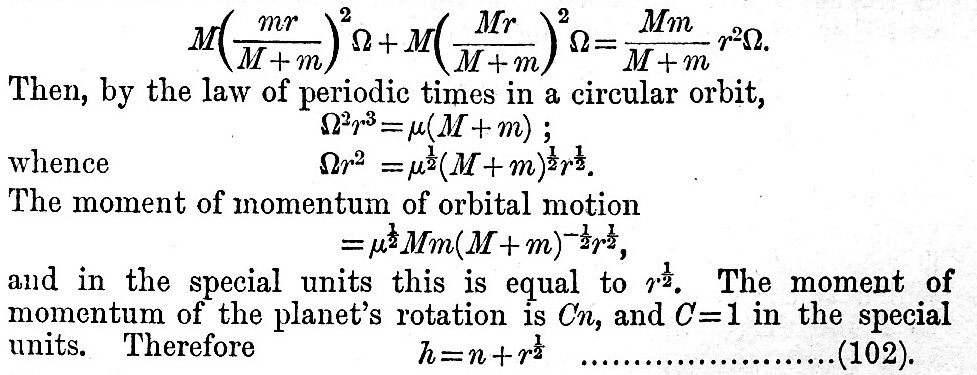
Since the moon’s present radius vector is 11·454, it follows that the orbital momentum of the moon is 3·384. Adding to this the rotational momentum of the earth, which is ·704, we obtain 4·088 for the total moment of momentum of the moon and earth. The ratio of the orbital to the rotational momentum is 4·80, so that the total moment of momentum of the system would, but for the obliquity of the ecliptic, be 5·80 times that of the earth’s rotation. Again, the kinetic energy of orbital motion is
The kinetic energy of the planet’s rotation is 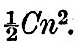 The potential energy of the system is - μMm/r. Adding the three energies together, and transforming into the special units, we have The potential energy of the system is - μMm/r. Adding the three energies together, and transforming into the special units, we have
It will be noticed that x, the moment of momentum of orbital motion, is equal to the square root of the satellite’s distance from the planet. Then equations (102) and (103) become
(104) is the equation of conservation of moment of momentum, or, shortly, the equation of momentum; (105) is the equation of energy.
Now consider a system started with given positive moment of momentum h; and we have all sorts of ways in which it may be started. If the two rotations be opposite kinds, it is clear that we may start the system with any amount of energy however great, but the true maxima and minima of energy compatible with the given moment of momentum are supplied by dY/dx = 0, or
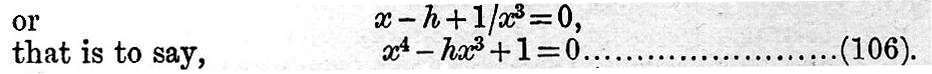
We shall presently see that this quartic has either two real roots and two imaginary, or all imaginary roots. The quartic may be derived from quite a different consideration, viz., by finding the condition under which the satellite may move round the planet so that the planet shall always show the same face to the satellite, - in fact, so that they move as parts of one rigid body. The condition is simply that the satellite’s orbital angular velocity Ω = n, the planet’s angular velocity of rotation, or y = 1/x3, since n = y and 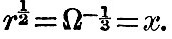 By substituting this value of y in the equation of momentum (104), we get as before By substituting this value of y in the equation of momentum (104), we get as before
At present we have only obtained one result, viz., that, if with given moment of momentum it is possible to set the satellite and planet moving as a rigid body, it is possible to do so in two ways, and one of these ways requires a maximum amount of energy and the other a minimum; from this it is clear that one must be a rapid rotation with the satellite near the planet and the other a slow one with the satellite remote from the planet. In the three equations
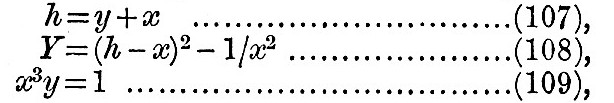
(107) is the equation of momentum, (108) that of energy, and (109) may be called the equation of rigidity, since it indicates that the two bodies move as though parts of one rigid body. To illustrate these equations geometrically, we may take as abscissa x, which is the moment of momentum of orbital motion, so that the axis of x may be called the axis of orbital momentum. Also, for equations (107) and (109) we may take as ordinate y, which is the moment of momentum of the planet’s rotation, so that the axis of y may be called the axis of rotational momentum. For (108) we may take as ordinate Y, which is twice the energy of the system, so that the axis of Y may be called the axis of energy. Then as it will be convenient to exhibit all three curves in the same figure, with a parallel axis of x, we must have the axis of energy identical with that of rotational momentum. It will not be necessary to consider the case where the resultant moment of momentum h is negative, because this would only be equivalent to reversing all the rotations; h is therefore to be taken as essentially positive. Then the line of momentum whose equation is (107) is a straight line inclined at 45° to either axis, having positive intercepts on both axes. The curve of rigidity whose equation is (109) is clearly of the same nature as a rectangular hyperbola, but it has a much more rapid rate of approach to the axis of orbital momentum than to that of rotational momentum. The intersections (if any) of the curve of rigidity with the line of momentum have abscissae which are the two roots of the quartic x4 – hx3 + 1 = 0. The quartic has, therefore, two real roots or all imaginary roots. Then, since 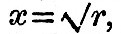 the intersection which is more remote from the origin indicates a configuration where the satellite is remote from the planet; the other gives the configuration where the satellite is closer to the planet. We have already learnt that these two correspond respectively to minimum and maximum energy. When x is very large, the equation to the curve of energy is Y = (h - x)2, which is the equation to a parabola with a vertical axis parallel to Y and distant h from the origin, so that the axis of the parabola passes through the intersection of the line of momentum with the axis of orbital momentum. When x is very small, the equation becomes Y = -1/x2. Hence the axis of Y is asymptotic on both sides to the curve of energy. Then, if the line of momentum intersects the curve of rigidity, the curve of energy has a maximum vertically underneath the point of intersection nearer the origin and a minimum underneath the point more remote. But, if there are no intersections, it has no maximum or minimum. the intersection which is more remote from the origin indicates a configuration where the satellite is remote from the planet; the other gives the configuration where the satellite is closer to the planet. We have already learnt that these two correspond respectively to minimum and maximum energy. When x is very large, the equation to the curve of energy is Y = (h - x)2, which is the equation to a parabola with a vertical axis parallel to Y and distant h from the origin, so that the axis of the parabola passes through the intersection of the line of momentum with the axis of orbital momentum. When x is very small, the equation becomes Y = -1/x2. Hence the axis of Y is asymptotic on both sides to the curve of energy. Then, if the line of momentum intersects the curve of rigidity, the curve of energy has a maximum vertically underneath the point of intersection nearer the origin and a minimum underneath the point more remote. But, if there are no intersections, it has no maximum or minimum.
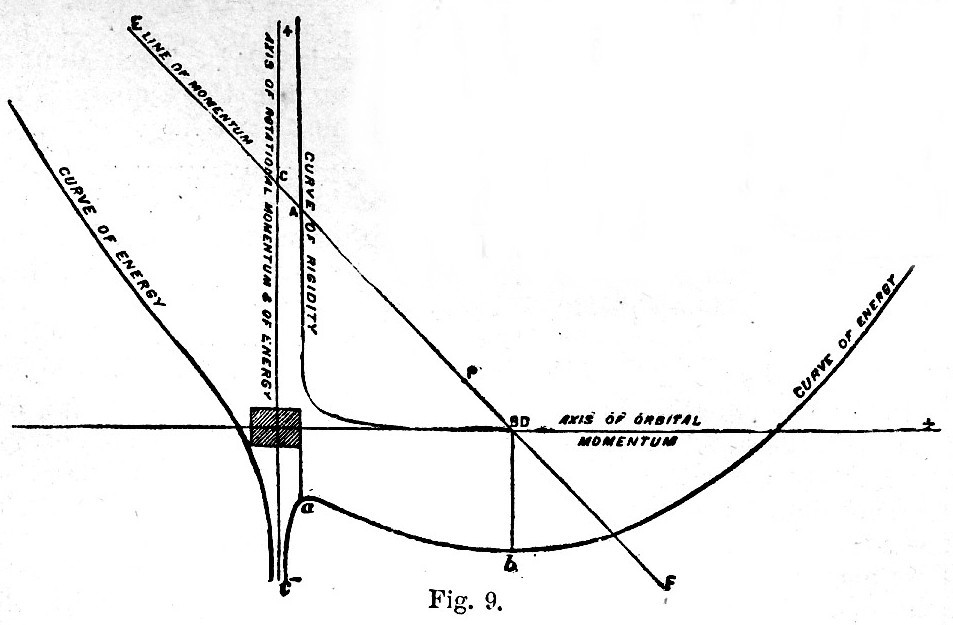
Fig. 9 shows these curves when drawn to scale for the case of the earth and moon, that is to say, with h = 4. The points a and b, which are the maximum and minimum of the curve of energy, are supposed to be on the same ordinates as A and B, the intersections of the curve of rigidity with the line of momentum. The intersection of the line of momentum with the axis of orbital momentum is denoted by D, but in a figure of this size it necessarily remains indistinguishable from B. As the zero of energy is quite arbitrary, the origin for the energy curve is displaced downwards, and this prevents the two curves from crossing one another in a confusing manner. On account of the limitation imposed we neglect the case where the quartic has no real roots. Every point of the line of momentum gives by its abscissa and ordinate the square root of the satellite’s distance and the rotation of the planet, and the ordinate of the energy curve gives the energy corresponding to each distance of the satellite. Part of the figure has no physical meaning, for it is impossible for the satellite to move round the planet at a distance less than the sum of the radii of the planet and satellite. For example, the moon’s diameter being about 2200 miles, and the earth’s about 8000, the moon's distance cannot be less than 5100 miles. Accordingly a strip is marked off and shaded on each side of the vertical axis within which the figure has no physical meaning. The point P indicates the present configuration of the earth and moon. The curve of rigidity x3y = l is the same for all values of h, and by moving the line of momentum parallel to itself nearer to or further from the origin, we may represent all possible moments of momentum of the whole system. The smallest amount of moment of momentum with which it is possible to set the system moving as a rigid body, with centrifugal force enough to balance the mutual attraction, is when the line of momentum touches the curve of rigidity. The condition for this is clearly that the equation x4 – hx3 + 1 = 0 should have equal roots. If it has equal roots, each root must be 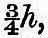 and therefore and therefore
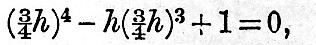
whence 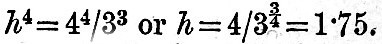 The actual value of h for the moon and earth is about 4; hence, if the moon-earth system were started with less than The actual value of h for the moon and earth is about 4; hence, if the moon-earth system were started with less than 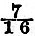 of its actual moment of momentum, it would not be possible for the two bodies to move so that the earth should always show the same face to the moon. Again, if we travel along the line of momentum, there must be some point for which yx3 is a maximum, and since yx3 = n/Ω there must be some point for which the number of planetary rotations is greatest during one revolution of the satellite; or, shortly, there must be some configuration for which there is a maximum number of days in the month. Now yx3 is equal to x3(h - x), and this is a maximum when of its actual moment of momentum, it would not be possible for the two bodies to move so that the earth should always show the same face to the moon. Again, if we travel along the line of momentum, there must be some point for which yx3 is a maximum, and since yx3 = n/Ω there must be some point for which the number of planetary rotations is greatest during one revolution of the satellite; or, shortly, there must be some configuration for which there is a maximum number of days in the month. Now yx3 is equal to x3(h - x), and this is a maximum when 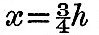 and the maximum number of days in the month is and the maximum number of days in the month is 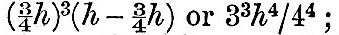 if h is equal to 4, as is nearly the case for the earth and moon, this becomes 27. Hence it follows that we now have very nearly the maximum number of days in the month. A more accurate investigation in a paper on the "Precession of a Viscous Spheroid" in Phil. Trans., part i., 1879, showed that, taking account of solar tidal friction and of the obliquity to the ecliptic, the maximum number of days is about 29, and that we have already passed through the phase of maximum. We will now consider the physical meaning of the figure. It is assumed that the resultant moment of momentum of the whole system corresponds to a positive rotation. Now imagine two points with the same abscissa, one on the momentum line and the other on the energy curve, and suppose the one on the energy curve to guide that on the momentum line. Then, since we are supposing frictional tides to be raised on the planet, the energy must degrade, and however the two points are set initially the point on the energy curve must always slide down a slope, carrying with it the other point. Looking at the figure, we see that there are four slopes in the energy curve, two running down to the planet and two down to the minimum. There are therefore four ways in which the system may degrade, according to the way it was started; but we shall only consider one, that corresponding to the portion ABba of the figure. For the part of the line of momentum AB the month is longer than the day, and this is the case with all known satellites except the nearer one of Mars. Now, if a satellite be placed in the condition A—that is to say, moving rapidly round a planet which always shows the same as face to the satellite—the condition is clearly dynamically unstable, for the least disturbance will determine whether the system shall degrade down the slopes ac or ab—that is to say, whether it falls into or recedes from the planet. If the equilibrium breaks down by the satellite receding, the recession will go on until the system has reached the state corresponding to B. It is clear that, it the intersection of the edge of the shaded strip with the line of momentum be identical with the point A, which indicates that the satellite is just touching the planet, then the two bodies are in effect parts of a single body in an unstable configuration. If, therefore, the moon was originally part of the earth, we should expect to find this identity. Now in fig. 9, drawn to scale to re-present the earth and moon, there is so close an approach between the edge of the shaded band and the intersection of the line of momentum and curve of rigidity that it would be scarcely possible to distinguish them. Hence, there seems a probability that the two bodies once formed parts of a single one, which broke up in consequence of some kind of instability. This view is confirmed by the more detailed consideration of the case in the paper on the "Precession of a Viscous Spheroid," already referred to and subsequent papers, in the Philosophical Transactions of the Royal Society. [Footnote 376-1] if h is equal to 4, as is nearly the case for the earth and moon, this becomes 27. Hence it follows that we now have very nearly the maximum number of days in the month. A more accurate investigation in a paper on the "Precession of a Viscous Spheroid" in Phil. Trans., part i., 1879, showed that, taking account of solar tidal friction and of the obliquity to the ecliptic, the maximum number of days is about 29, and that we have already passed through the phase of maximum. We will now consider the physical meaning of the figure. It is assumed that the resultant moment of momentum of the whole system corresponds to a positive rotation. Now imagine two points with the same abscissa, one on the momentum line and the other on the energy curve, and suppose the one on the energy curve to guide that on the momentum line. Then, since we are supposing frictional tides to be raised on the planet, the energy must degrade, and however the two points are set initially the point on the energy curve must always slide down a slope, carrying with it the other point. Looking at the figure, we see that there are four slopes in the energy curve, two running down to the planet and two down to the minimum. There are therefore four ways in which the system may degrade, according to the way it was started; but we shall only consider one, that corresponding to the portion ABba of the figure. For the part of the line of momentum AB the month is longer than the day, and this is the case with all known satellites except the nearer one of Mars. Now, if a satellite be placed in the condition A—that is to say, moving rapidly round a planet which always shows the same as face to the satellite—the condition is clearly dynamically unstable, for the least disturbance will determine whether the system shall degrade down the slopes ac or ab—that is to say, whether it falls into or recedes from the planet. If the equilibrium breaks down by the satellite receding, the recession will go on until the system has reached the state corresponding to B. It is clear that, it the intersection of the edge of the shaded strip with the line of momentum be identical with the point A, which indicates that the satellite is just touching the planet, then the two bodies are in effect parts of a single body in an unstable configuration. If, therefore, the moon was originally part of the earth, we should expect to find this identity. Now in fig. 9, drawn to scale to re-present the earth and moon, there is so close an approach between the edge of the shaded band and the intersection of the line of momentum and curve of rigidity that it would be scarcely possible to distinguish them. Hence, there seems a probability that the two bodies once formed parts of a single one, which broke up in consequence of some kind of instability. This view is confirmed by the more detailed consideration of the case in the paper on the "Precession of a Viscous Spheroid," already referred to and subsequent papers, in the Philosophical Transactions of the Royal Society. [Footnote 376-1]
Footnote
376-1 For further consideration of this subject see a series of papers by Mr G. H. Darwin, in Proceed. and Trans. of the Royal Society from 1878 to 1881, and Appendix G (b) to part ii. vol. i. of Thomson and Tait’s Nat. Phil., 1883.
Read the rest of this article:
Tides - Table of Contents
|