IX. TIDAL FRICTION (cont.)
48. Amount of Tidal Retardation of Earth’s Rotation
With respect to the actual amount of retardation of the earth’s rotation, we quote the following from Thomson and Tait’s Nat. Phil. (1883), § 830. [Footnote 377-1]
"In observational astronomy the earth’s rotation serves as a time-keeper, and thus a retardation of terrestrial rotation will appear astronomically as an acceleration of the motion of the heavenly bodies. It is only in the case of the moon’s motion that such an apparent acceleration can be possibly detected. Now, as Laplace first pointed out, there must be a slow variation in the moon’s mean motion arising from the secular changes in the eccentricity of the earth’s orbit around the sun. At the present time, and for several thousand years in the future, the variation in the moon’s motion is and will be an acceleration. Laplace’s theoretical calculation of the amount of that acceleration appeared to agree well with the results which were in his day accepted as representing the facts of observation. But in 1853 Adams showed that Laplace’s reasoning was at fault, and that the numerical results of Damoiseau’s and Plana’s theories with reference to it consequently require to be sensibly altered. Hansen’s theory of the secular acceleration is vitiated by an error of principle similar to that which affects the theories of Damoiseau and Plana; but, the mathematical process which he followed being different from theirs, he arrived at somewhat different results. From the erroneous theory Hansen found the value of 12″·18 for the coefficient of the term in the moon’s mean longitude depending on the square of the time, the unit of time being a century; in a later computation given in his Darlegung he found the coefficient to be 12″·56. [Footnote 377-2]
"In 1859 Adams communicated to Delaunay his final result, namely, that the coefficient of this term appears from a correctly conducted investigation to be 5″·7, so that at the end of a century the moon is 5″·7 before the position it would have had at the same time if its mean angular velocity had remained the same as at the beginning of the century. Delaunay verified this result, and added some further small terms which increased the coefficient from 5″·7 to 6″·l.
"Now, according to Airy, Hansen’s value of the ‘advance’ represents very well the circumstances of the eclipses of Agathocles, of Larissa, and Thales, but is if anything too small. Newcomb, on the other hand, is inclined from an elaborate discussion of the ancient eclipses to believe Hansen’s value to be too large, and gives two competing values, viz., 8″·4 and 10″·9. [Footnote 377-3]
"In any case it follows that the value of the advance as theoretically deduced from all the causes, known up to the present time to be operative, is smaller than that which agrees with observation. In what follows 12″ is taken as the observational value of the advance, and 6″ as the explained part of this phenomenon. About the beginning of 1866 Delaunay suggested that the true explanation of the discrepancy might be a retardation of the earth’s rotation by tidal friction. Using this hypothesis, and allowing for the consequent retardation of the moon’s mean motion by tidal reaction, Adams, in an estimate which he has communicated to us, founded on the rough assumption that the parts of the earth’s retardation due to solar and lunar tides are as the squares of the respective tide-generating forces, finds 22 sec. as the error by which the earth, regarded as a time-keeper, would in a century get behind a perfect clock rated at the beginning of the century. Thus at the end of a century a meridian of the earth is 330″ behind the position in which it would have been if the earth had continued to rotate with the same angular velocity which it had at the beginning of the century. . .
"Whatever be the value of the retardation of the earth’s rotation it is necessarily the result of several causes, of which tidal friction is almost certainly preponderant. If we accept Adams’s estimate as applicable to the outcome of the various concurring causes, then, if the rate of retardation giving the integral effect were uniform, the earth as a time-keeper would be going slower by ·22 of a second per year in the middle, and by ·44 of a second per year at the end, than at the beginning of the century. The latter is 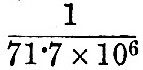 of the present angular velocity; and, if the rate of retardation had been uniform during ten million centuries past, the earth must have been rotating faster by about one-seventh than at present, and the centrifugal force must have been greater in the proportion of 8172 to 7172 or of 67 to 51. If the consolidation took place then or earlier, so the ellipticity of the upper layers must have been
of the present angular velocity; and, if the rate of retardation had been uniform during ten million centuries past, the earth must have been rotating faster by about one-seventh than at present, and the centrifugal force must have been greater in the proportion of 8172 to 7172 or of 67 to 51. If the consolidation took place then or earlier, so the ellipticity of the upper layers must have been 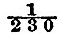 instead of about
instead of about 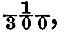 , as it is at present. It must necessarily remain uncertain as whether the earth would from time to time adjust itself completely of to a figure of equilibrium adapted to the rotation. But it is clear so that a want of complete adjustment would leave traces in a preponderance of land in equatorial regions. The existence of large continents and the great effective rigidity of the earth’s mass render it improbable that the adjustments, if any, to the appropriate figure of equilibrium would be complete. The fact then that the continents are arranged along meridians rather than in an equatorial belt affords some degree of proof that the consolidation of the earth took place at a time when the diurnal rotation differed but little from its present value. It is probable, therefore, that the date of consolidation is considerably more recent than a thousand million years ago. It is proper, however, to add that Adams lays but little stress on the actual numerical values which have been used in this computation, and is of opinion that the amount of tidal retardation of the earth’s rotation is quite uncertain."
, as it is at present. It must necessarily remain uncertain as whether the earth would from time to time adjust itself completely of to a figure of equilibrium adapted to the rotation. But it is clear so that a want of complete adjustment would leave traces in a preponderance of land in equatorial regions. The existence of large continents and the great effective rigidity of the earth’s mass render it improbable that the adjustments, if any, to the appropriate figure of equilibrium would be complete. The fact then that the continents are arranged along meridians rather than in an equatorial belt affords some degree of proof that the consolidation of the earth took place at a time when the diurnal rotation differed but little from its present value. It is probable, therefore, that the date of consolidation is considerably more recent than a thousand million years ago. It is proper, however, to add that Adams lays but little stress on the actual numerical values which have been used in this computation, and is of opinion that the amount of tidal retardation of the earth’s rotation is quite uncertain."
Footnotes
377-1 See also G. H. Darwin's Address to Sect. A, Brit. Assoc. meeting, 1886.
377-2 "It appear not unusual for physical astronomer to use an abbreviated phraseology, for specifying accelerations, which needs explanation. Thus, when they speak of the secular acceleration being, e.g. '12″·26 in a century,' they mean by 'acceleration' what is more properly 'the effect of acceleration on the moon's mean longitude.' The correct unabbreviated statement is 'the acceleration is 25″·12 per century per century.' Thus Hansen's result is that in each century the mean motion of the moon is augmented by an angular velocity of 25″·12 per century, so that at the end of a century the mean longitude is greater by ½ of 25″·12 than it would have been had the moon's mean motion remained the same as it was at the beginning of the century. Considering how absurd it would be to speak of a falling body as experiencing an acceleration of 16 feet in a second, or of 64 feet in two seconds, and how false and inconvenient it is to speak of a watch being 20 seconds fast when it is 20 seconds in advance of where it ought to be, we venture to suggest that, to attain clearness and correctness without sacrifice of brevity, 'advance' to be substituted by 'acceleration' in the ordinary astronomical phraseology."
377-3 Researches on the Motion of the Moon, Washington, 1878.
Read the rest of this article:
Tides - Table of Contents