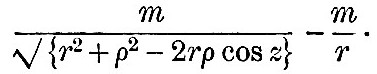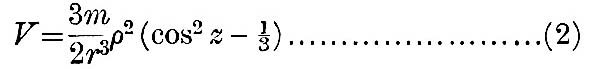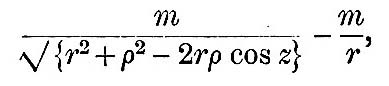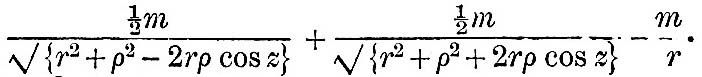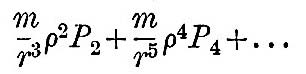II. TIDE-GENERATING FORCES

5. Investigation of Tide-Generating Potential and Forces

Tide-Generating Forces

We have already given a general explanation of the nature of tide-generating forces; we now proceed to a rigorous investigation.

If a planet is attended by a single satellite, the motion of any body relatively to the planet’s surface is found by the process described as reducing the planet’s centre to rest. The planet’s centre will be at rest if every body in the system has impressed on it a velocity equal and opposite to that of the planet’s centre; and this is accomplished by impressing on every body an acceleration equal and opposite to that of the planet’s centre.

Let M, m be the masses of the planet and the satellite; r the radius vector of the satellite, measured from the planet’s centre; &rho the radius vector, measured from the same point, of the particle whose motion we wish to determine; and z the angle between r and &rho . The satellite moves in an elliptic orbit about the planet, and the acceleration relatively to the planet’s centre of the satellite is (M + m)/r² towards the planet along the radius vector r. Now the centre of inertia of the planet and satellite remains fixed in space, and the centre of the planet describes an orbit round that centre of inertia similar to that described by the satellite round the planet, but with linear dimensions reduced in the proportion of m to M + m. Hence the acceleration of the planet’s centre is m/r² towards the centre of inertia of the two bodies. Thus, in order to reduce the planet’s centre to rest, we apply to every particle of the system an acceleration m/r² parallel to r, and directed from satellite to planet.

Now take a set of rectangular axes fixed in the planet, and let M₁r, M₂r, M₃r be the coordinates of the satellite referred thereto; and let ξρ, ηρ, ζρ be the coordinates of the particle P whose radius is ρ. Then the component accelerations for reducing the planet's centre to rest are – mM₁/r², – mM₂/r², – mM₃/r²; and since these are the differential coefficients with respect to ρξ, ρη, ρζ of the function

and since cos z = M₁ξ + M₂η +M₃ζ, it follows that the potential of the forces by which the planet’s centre is to be reduced to rest is

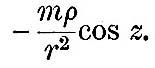
Now let us consider the other forces acting on the particle. The planet is spheroidal, and therefore does not attract equally in all directions; but in this investigation we may make abstraction of the ellipticity of the planet and of the ellipticity of the ocean due to the planetary rotation. This, which we set aside, is considered in the theories of gravity and of the figures of planets. Outside of its body, then, the planet contributes forces of which the potential is M/ρ. Next the direct attraction of the satellite contributes forces of which the potential is the mass of the satellite divided by the distance between the point P and the satellite; this is—

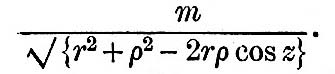
To determine the forces from this potential we regard ρ and z as the variables for differentiation, and we may add to this potential any constant we please. As we are seeking to find the forces which urge P relatively to M, we add such a constant as will make the whole potential at the planet’s centre zero, and thus we take as the potential of the forces due to the attraction of the satellite —

It is obvious that r is very large compared with ρ, and we may therefore expand this in powers of ρ/r. This expansion gives us

where

The reader familiar with spherical harmonic analysis of course recognizes the Legendre’s functions; but the result for a few terms, which is all that is necessary, is easily obtainable by simple algebra.

Potential

Now, collecting together the various contributions to the potential, and noticing that

and is therefore equal and opposite to the potential by which the planet’s centre was reduced to rest, we have as the potential of the forces acting on a particle whose coordinates are ρξ, ρη, ρζ

The first term of (1) is the potential of gravity, and the terms of the series, of which two only are written, constitute the tide-generating potential. In all practical applications this series converges so rapidly that the first term is amply sufficient, and thus we shall generally denote

as the tide-generating potential.

In many mathematical works the tide-generating force is presented as being due to an artificial statical system, which produces nearly the same force as the dynamical system considered above. This statical system is as follows. Stopping all the rotations, we divide the satellite into two equal parts, and place them diametrically opposite to one another in the orbit. Then it is clear that, instead of the term

And this reduces to

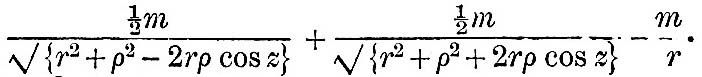
The first term is the same as before; hence the statical system produces approximately the same tide-generating force as the true system. The "moon" and "anti-moon," however, produce rigorously the same force on each side of the planet, whereas the true system only satisfies this condition approximately. [Footnote 356-1]






Footnote

356-1 The reader may refer to Thomson and Tait’s Natural Philosophy (1883), part ii. §§ 798-821, for further considerations on this and analogous subjects, together with some interesting examples.



Read the rest of this article:
Tides - Table of Contents