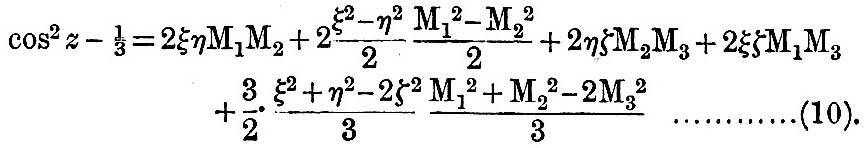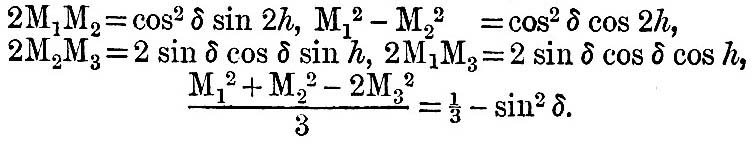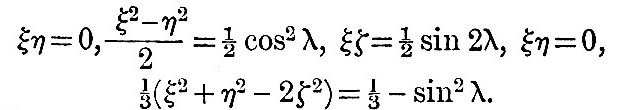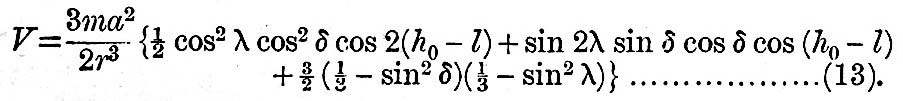1902 Encyclopedia > Tides > [Tide-Generating Forces] Development of Tide-Generating Potential in Terms of Hour-Angle and Declination
Tides
(Part 7)
II. TIDE-GENERATING FORCES (cont.)
7. Development of Tide-Generating Potential in Terms of Hour-Angle and Declination
We now proceed to develop the tide-generating potential, and shall of course implicitly (§ 6) determine the equation to the equilibrium figure.
We have already seen that, if z be the moon’s zenith distance at the point P on the earth’s surface, whose coordinates referred to A, B, C, axes fixed in the earth, are αξ, αη, αζ, then
Where M1, M2, M3, are the moon’s direction cosines referred to the same axes. Then with this value of cos z—
The axis of C is taken as the polar axis, and AB is the equatorial plane, so that the functions of ξ, η, ζ, are functions of the latitude and longitude of the point P, at which we wish to find the potential.
The functions of M1, M2, M3, depend on the moon’s position, and we shall have occasion to develop them in two different ways,— first in terms of her hour-angle and declination, and secondly (§ 23) in terms of her longitude and the elements of the orbit.
Now let A be on the equator in the meridian of P, and B 90° east of A on the equator. Then, if M be the moon, the inclination of the plane MC to the plane CA is the moon’s easterly local hour-angle. Let h = local hour-angle of moon and δ = moon’s declination: we have
M1 = cosδcosh, M2 = cosδsinh, M3 = sin δ
Also, if λ be the latitude of P,
ξ = cos λ, η = 0, ζ = sin λ,
The angle h, as defined at present, is the eastward local hour-angle, and therefore diminishes with the time. As, however, this function does not change sign with h, it will be more convenient to regard it as the westward local hour-angle. Also, if h0, be the Greenwich westward hour-angle at the moment under consideration, and l be the west longitude of the place of observation P, we have
h =h0 – l.................................................(12).
Hence we have at the point P, whose radius vector is α,
The tide-generating forces are found by the rates of variation of V for latitude and longitude, and also for radius α, if we care to find the radial disturbing force.
Read the rest of this article:
Tides - Table of Contents
|