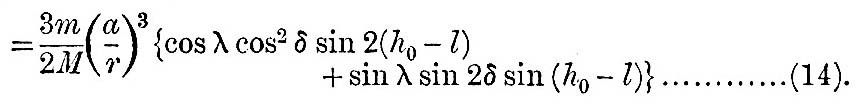1902 Encyclopedia > Tides > [Tide-Generating Forces] Evaluation of Tide-Generating Forces, and Lunar Deflexion of Gravity
Tides
(Part 8)
II. TIDE-GENERATING FORCES (cont.)
8. Evaluation of Tide-Generating Forces, and Lunar Deflexion of Gravity
The westward component of the tide-generating force at the earth's surface, where ρ = α, is dV/α cos λdl, and the northward component is dV/adλ ; the change of apparent level is the ratio of these to gravity g. Therefore, differentiating (13), changing signs, and writing
we have component change of level southward
component change of level westward
The westward component is made up of two periodic terms, one going through its variations twice and the other once a day. The southward component has also two similar terms; but it has a third term; which does not oscillate about a zero value. If Δ be a declination such that the mean value of sin2 δ is equal to sin2 Δ, then, to determine the southward component so that it shall be a truly periodic function, we must subtract from the above sin 2λ(1 - 3 sin2 Δ), and the last term then becomes
3 sin 2λ(sin2 Δ – sin2 δ).
In the case of the moon, Δ varies a little according to the position of the moon’s node, but its mean value is about 16° 31'.
The constant portion of the southward component of force has its effect in causing a constant heaping up of the water at the equator; or, in other words, the moon’s attraction has the effect of causing a small permanent ellipticity of the earth’s mean figure. This augmentation of ellipticity is of course very small, but it is necessary to mention it in order that the meaning to be attributed to lunar deflexion of gravity may be clearly defined.
If we consider the motion of a pendulum-bob during any one day, we see that, in consequence of the semi-diurnal changes of level, it twice describes an ellipse with major axis east and west, with ratio of axes equal to the sine of the latitude, and with linear dimensions proportional to cos2 δ, and it once describes an ellipse whose north and south axis is proportional to sin 2δ cos 2λ and whose east and west axis is proportional to sin 2δ sin λ. Obviously the latter is circular in latitude 30°. When the moon is on the equator, the maximum deflexion occurs when the moon’s local hour-angle is 45º, and is then equal to
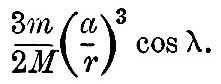
At Cambridge in latitude 52° 43' this angle is 0"·0216.
An attempt, made by George and Horace Darwin, [Footnote 358-1] to measure the lunar deflexion of a pendulum failed on account of incessant variability of level occurring in the supports of the pendulum and arising from unknown terrestrial changes. The work done, therefore, was of no avail for the purposes for which it was instituted, but remained as a contribution to an interesting subject now beginning to be studied, viz., the small changes which are always taking place on the upper strata of the earth.
Footnote
359-1 Reports to the British Assoc., 1881 (York) and 1882 (Southampton).
Read the rest of this article:
Tides - Table of Contents
|