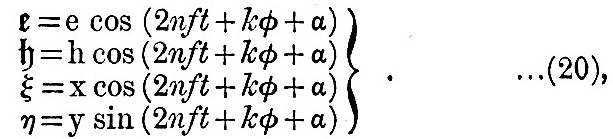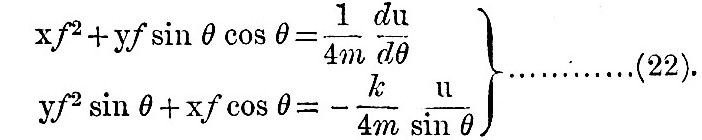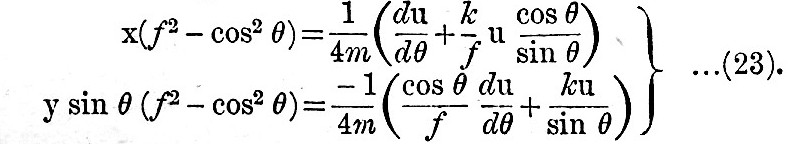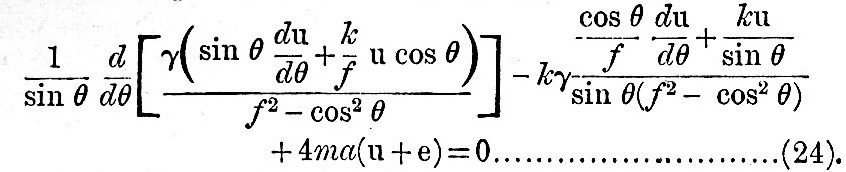III. DYNAMICAL THEORY OF TIDES (cont.)
12. Adaptation to Forced Oscillations
Since we may suppose that the free oscillations are annulled by friction, the solution required is that corresponding to forced oscillations. Now we have seen from (13) that  (which is proportional to V) has terms of three kinds, the first depending on twice the moon’s (or sun’s) hour-angle, the second on the hour-angle, and the third independent thereof. The coefficients of the first and second terms vary slowly, and the whole of the third varies slowly. Hence
(which is proportional to V) has terms of three kinds, the first depending on twice the moon’s (or sun’s) hour-angle, the second on the hour-angle, and the third independent thereof. The coefficients of the first and second terms vary slowly, and the whole of the third varies slowly. Hence  has a semi-diurnal, a diurnal, and a long period term. We shall see later that these terms may be expanded in a series of approximately semi-diurnal, diurnal, and slowly varying terms, each of which is a strictly harmonic function of the time. Thus we may assume for
has a semi-diurnal, a diurnal, and a long period term. We shall see later that these terms may be expanded in a series of approximately semi-diurnal, diurnal, and slowly varying terms, each of which is a strictly harmonic function of the time. Thus we may assume for  a form e cos (2nft + kφ + a), where f and k are numbers, and where e is only a function of co-latitude and of the elements of the orbit of the disturbing body. According to the usual method of treating oscillating systems, we may therefore make the following assumption for the form of solution
a form e cos (2nft + kφ + a), where f and k are numbers, and where e is only a function of co-latitude and of the elements of the orbit of the disturbing body. According to the usual method of treating oscillating systems, we may therefore make the following assumption for the form of solution
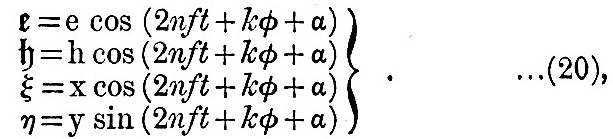
where e, h, x, y are functions of co-latitude θ only. Substituting these values in (19), we have
Then, if we write u for h - e, and put m = n2a/g, substitution from (20) in (17) leads at once to
Solving (22) for x and y, we have
Then substituting from (23) in (21), we have
This is Laplace’s equation for tidal oscillations in an ocean whose depth is only a function of latitude. When u is found from this equation, its value substituted in (23) will give x and y.
Read the rest of this article:
Tides - Table of Contents