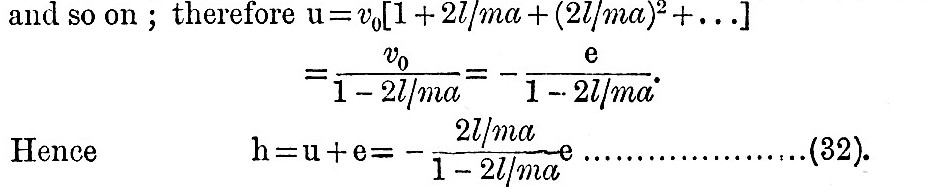|
1902 Encyclopedia > Tides > [Dynamical Theory of Tides] Semi-Diurnal Tide, with Variable Depth Tides
|
About this Encyclopedia • Top Contributors • All Contributors • Today in History Sitemaps • Terms of Use • Privacy • Contact Us © 2005-25 1902 Encyclopedia. All Rights Reserved. This website is the free online Encyclopedia Britannica (9th Edition and 10th Edition) with added expert translations and commentaries |