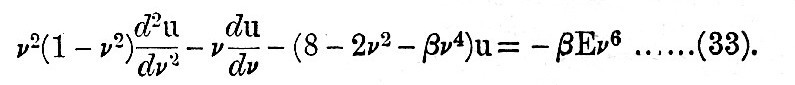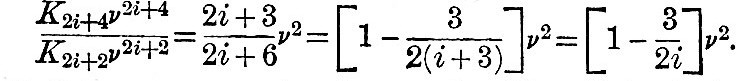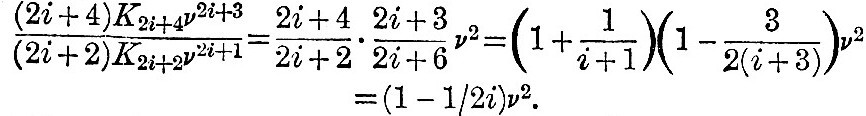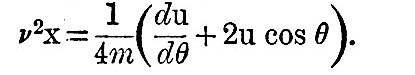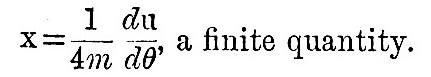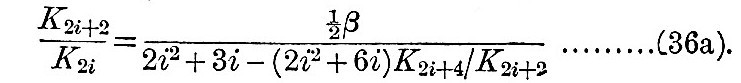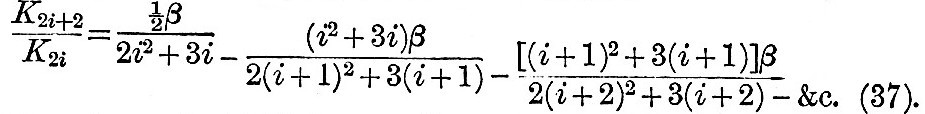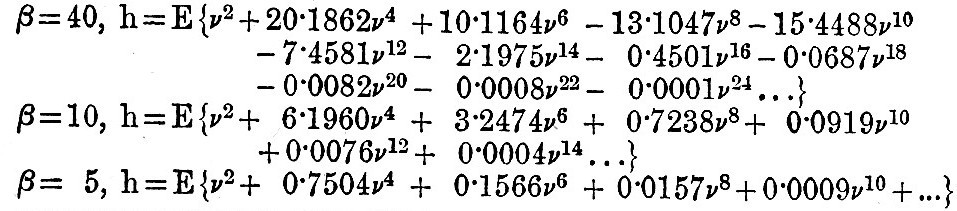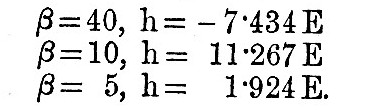1902 Encyclopedia > Tides > [Dynamical Theory of Tides] Semi-Diurnal Tide, with Uniform Depth
Tides
(Part 16)
III. DYNAMICAL THEORY OF TIDES (cont.)
16. Semi-Diurnal Tide, with Uniform Depth
The method of development used above, where we proceed by powers of the depth of the ocean, is not applicable where the depth is uniform, because it leads to a divergent series. We have therefore to resume equation (24). In the case of the semi-diurnal tides we have for the depth γ = l (a constant by hypothesis), k = 2, f = 1 approximately, and e = E sin2 θ. Now for brevity let β = 4ma/l, v = sin θ, so that e = Ev2. Then we find that on development (24) becomes
Let us now assume as the solution of this equation
Substituting from (34) in (33), and equating to zero the coefficients of the successive powers of v, we find K2 = E, K4 apparently indeterminate, and
Since K0 = 0, this equation of condition may be held to apply for all positive integral values of i, beginning with i = 0. It is obvious that K6 is determinable in terms of K4 and K2, K5 in terms of K6 and K4, &c., so that all the K's are to be found in terms of K2, which is known, and of K4, which is apparently indeterminate.
The condition for the convergency of the series (34) for u and for the series du/dv is that K2i+2/K2i shall tend to a limit less than unity. The equation (35) may be written
Now K2i+2/K2i tends to be either infinitely small or not infinitely small. If it be not infinitely small in the limit, the second term on the right of (36) becomes evanescent when i is very great, and we have in the limit when i is very large—
Therefore at the equator, where v=l, du/dθ = D, a finite quantity. Hence the hypothesis that K2i+2/K2i tends to be not infinitely small leads to the conclusion that u and du/dθ are finite at the equator. But on account of the symmetry of the system the co-latitudinal displacement ξ must vanish at the equator, and therefore x also. By (23), when f = 1, k = 2, v = sinθ,
But we have just seen that this hypothesis makes u finite when v = 1 or θ = 90°, and therefore at the equator
Now symmetry necessitates a vanishing value of du/dθ at the equator. Thus the hypothesis that K2i+2/K2i tends to be not infinitely small is negatived, and we conclude that, on account of the symmetry of the motion, it is infinitely small for infinitely great values of i. This being established, let us write (36) in the form
Hence by repeated application of (36a) we have
And we know that this is a continuous approximation to K2i+2/K2i, which must hold in order that the latitudinal velocity may vanish at the equator. Writing Ni = K2i+2/K2i, all the N’s may be computed from the continued fraction (37). Then
K2=E, K4/E=N1, K6/E=N1N2, K8/E=N1N2N3, &c.
We cannot compute K6 from K4, K8 from K6, and so on; for, if we do, then, short of infinite accuracy in the numerical values, we shall be gradually led to successive values of the K’s which tend to equality.[Footnote 360-1]
This process was followed by Laplace without explanation. It was attacked by Airy in his "Tides and Waves" (in Ency. Metrop.) and by Ferrel in his Tidal Researches (U.S. Coast Survey, 1873), but was justified by Sir W. Thomson in the Phil. Mag. (1875, p. 230). The investigation given here is substantially Thomson’s.
Laplace gives numerical solutions for three different depths of the sea, 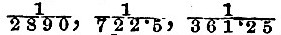 of the earth’s radius. Since of the earth’s radius. Since 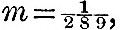 these correspond respectively to the cases of β=40, 10, 5, and the solutions are these correspond respectively to the cases of β=40, 10, 5, and the solutions are
Since h vanishes when v = 0, there is no rise and fall of water at the poles. When v = 1 at the equator, we find
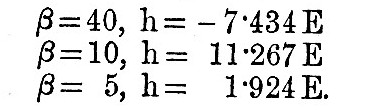
The negative sign in the first case shows that the tide is inverted at the equator, giving low water when the disturbing body is on the meridian. Near the pole, however, that is, for small values of v, the tides are direct. In latitude 18° (approximately) there is a nodal line of evanescent semi-diurnal tide. In the second and third cases the tides are everywhere direct, increasing in magnitude from pole to equator. As β diminishes the tides tend to assume their equilibrium value, because all the terms, save the first, become evanescent. When β = 1 (depth 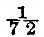 of radius) the tide at the equator still exceeds its equilibrium value by 11 per cent. As β diminishes from 40 to 10 the nodal line of evanescent tide contracts round the pole, and when it is infinitely small the tides are infinitely great. The particular value of β for which this occurs is that where the free oscillation of the ocean has the same period as the forced oscillation. The values chosen by Laplace were not well adapted for the illustration of the results, because in the cases of β = 40 and β = 10 the depth of the ocean is not much different from that value which would give infinite semi-diurnal tide. For values of β greater than 40 we should find other nodal lines dividing the sphere into regions of direct and inverted tides. We refer the reader to Sir W. Thomson’s papers for further details on this interesting point. of radius) the tide at the equator still exceeds its equilibrium value by 11 per cent. As β diminishes from 40 to 10 the nodal line of evanescent tide contracts round the pole, and when it is infinitely small the tides are infinitely great. The particular value of β for which this occurs is that where the free oscillation of the ocean has the same period as the forced oscillation. The values chosen by Laplace were not well adapted for the illustration of the results, because in the cases of β = 40 and β = 10 the depth of the ocean is not much different from that value which would give infinite semi-diurnal tide. For values of β greater than 40 we should find other nodal lines dividing the sphere into regions of direct and inverted tides. We refer the reader to Sir W. Thomson’s papers for further details on this interesting point.
Footnotes
360-1

Read the rest of this article:
Tides - Table of Contents
|