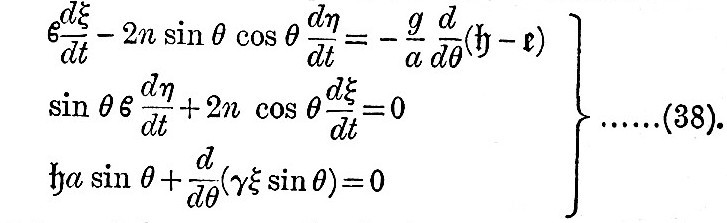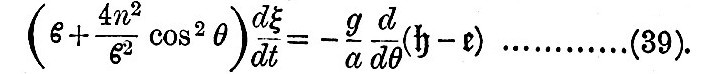III. DYNAMICAL THEORY OF TIDES (cont.)
17. Tides of Long Period; Laplace’s Argument from Friction
In treating these oscillations Laplace remarks that a very small amount of friction will be sufficient to cause the surface of the ocean to assume at each instant its form of equilibrium, and he adduces in proof of his conclusion the considerations given below. The friction here contemplated is such that the integral effect is represented by a retarding force proportional to the velocity of the water relatively to the bottom. Although proportionality to the square of the velocity would probably be nearer to the truth, yet Laplace’s hypothesis suffices for the present discussion.
In oscillations of this class the water moves for half a period north, and then for half a period south. In oscillating systems, where the resistances are proportional to the velocities, it is usual to specify the resistance by a modulus of decay, namely, that period in which a velocity is reduced to 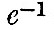 of its initial value by friction. Now the friction contemplated by Laplace is such that the modulus of decay is short compared with the semi-period of oscillation. The quickest of the important tides of long period is the fortnightly (see chapter iv.); hence, for the applicability of Laplace’s conclusion, the modulus of decay must be short compared with a week. Now it seems practically certain that the friction of the bed of the ocean would not materially affect the velocity of a slow ocean current in a day or two. Hence we cannot accept Laplace’s discussion as satisfactory. However this may be, we now give what is substantially his argument.
of its initial value by friction. Now the friction contemplated by Laplace is such that the modulus of decay is short compared with the semi-period of oscillation. The quickest of the important tides of long period is the fortnightly (see chapter iv.); hence, for the applicability of Laplace’s conclusion, the modulus of decay must be short compared with a week. Now it seems practically certain that the friction of the bed of the ocean would not materially affect the velocity of a slow ocean current in a day or two. Hence we cannot accept Laplace’s discussion as satisfactory. However this may be, we now give what is substantially his argument.
Let us write 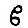 for the reciprocal of the modulus of decay. Then the frictional forces introduced on the left-hand side of (17) are
for the reciprocal of the modulus of decay. Then the frictional forces introduced on the left-hand side of (17) are 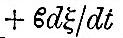 in the first and
in the first and 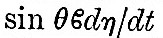 in the second. Laplace’s hypothesis with regard to the magnitude of the frictional forces enables us to neglect the terms d2ξ/dt2 and sin θ d2η/dt2 compared with the frictional forces. Then, if we observe that in oscillations of this class the motion is entirely latitudinal, equations (17) and (19) become
in the second. Laplace’s hypothesis with regard to the magnitude of the frictional forces enables us to neglect the terms d2ξ/dt2 and sin θ d2η/dt2 compared with the frictional forces. Then, if we observe that in oscillations of this class the motion is entirely latitudinal, equations (17) and (19) become