IV. HARMONIC ANALYSIS (cont.)
24. Meteorological Tides, Over-Tides, and Compound Tides
All tides whose period is an exact multiple or submultiple of a mean solar day, or of a tropical year, are affected by meteorological conditions. Thus all the tides of the principal solar astronomical series S, with speeds γ - η, 2(γ - η), 3(γ - η), &c., are subject to more or less meteorological perturbation. An annual inequality in the diurnal meteorological tide S1 will also give rise to a tide γ - 2η, and this will be fused with and indistinguishable from the astronomical P ; it will also give rise to a tide with speed γ, which will be indistinguishable from the astronomical part of K1. Similarly the astronomical tide K2 may be perturbed by a semiannual inequality in the semi-diurnal astronomical tide of speed 2(γ - η). Although the diurnal elliptic tide S1 or γ - η and the semi-annual and annual tides of speeds 2η and η are all probably quite insensible as arising from astronomical causes, yet they have been found of sufficient importance to be considered. The annual and semi-annual tides are of enormous importance in some rivers, representing in fact the yearly flooding in the rainy season. In the reduction of these tides the arguments of the S series are t, 2t, 3t, &c., and of the annual, semi-annual, ter-annual tides h, 2h, 3h. As far as can be foreseen, the magnitudes of these tides are constant from year to year.
We have in § 21 considered the dynamic theory of over tides. The only-tides of this kind in which it has hitherto been thought necessary to represent the change of form in shadow water belong to the principal lunar and principal solar series. Thus, besides the fundamental astronomical tides M2 and S2, the over-tides M4, M6, M8, and S4, S6 have been deduced by harmonic analysis. The height of the fundamental tide M2 varies from year to year, according to the variation in the obliquity of the lunar orbit, and this variability is represented by the coefficient 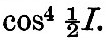 It is probable that the variability of M4, M6, M8 will be represented by the square, cube and fourth power of that coefficient, and theory (§ 21) indicates that we should make the argument of the over-tide a multiple of the argument of the fundamental, with a constant subtracted.
It is probable that the variability of M4, M6, M8 will be represented by the square, cube and fourth power of that coefficient, and theory (§ 21) indicates that we should make the argument of the over-tide a multiple of the argument of the fundamental, with a constant subtracted.
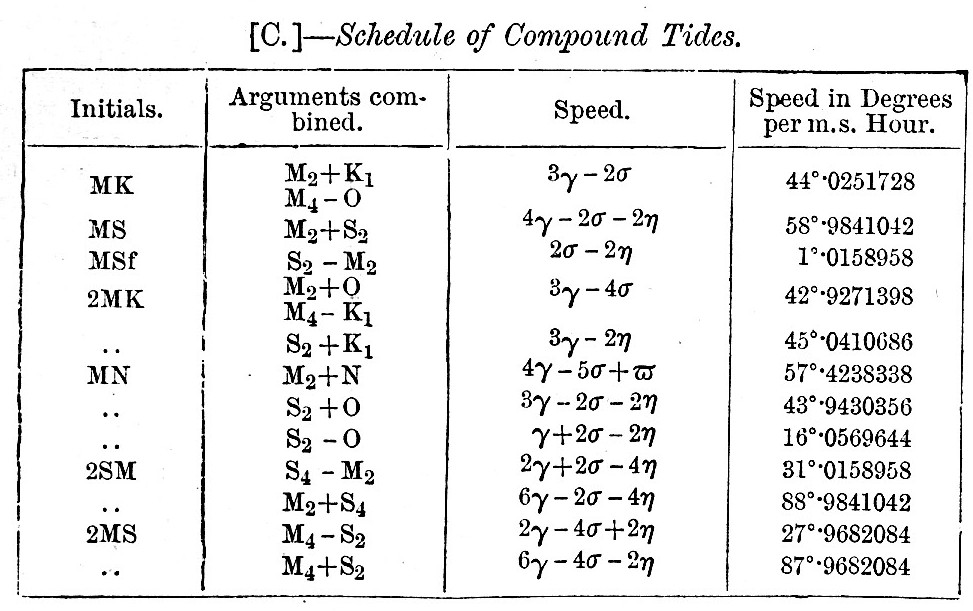
Compound tides have been also considered dynamically in §21. By combining the speeds of the important tides, it will be found that there is in many cases a compound tide which has itself a speed identical with that of an astronomical or meteorological tide. We thus find that the tides O, K1, Mm, P, M2, Mf, Q, M1, L are liable to perturbation in shallow water. If either or both the component tides are of lunar origin, the height of the compound tide will change from year to year, and will probably vary proportionally to the product of the coefficients of the component tides. For the purpose of properly reducing the numerical value of the compound tides, we require not merely the speed, but also the argument. The following schedule gives the adopted initials, argument, and speed of the principal compound tides. The coefficients are the products of those of the two tides to be compounded.