1902 Encyclopedia > Tides > [Harmonic Analysis] Numerical Harmonic Analysis for Tides of Short Period
Tides
(Part 26)
IV. HARMONIC ANALYSIS (cont.)
26. Numerical Harmonic Analysis for Tides of Short Period
The tide-gauge (described below, § 36) furnishes us with a continuous graphical record of the height of the water above some known datum mark for every instant of time. The first operation performed on the tidal record is the measurement in feet and decimals of the height of water above the datum at every mean solar hour. The period chosen for analysis is about one year and the first measurement corresponds to noon.
If T be the period of any one of the diurnal tides, or the double period of any one of the semi-diurnal tides, it approximates more or less nearly to 24 m.s. hours, and, if we divide it into twenty-four equal parts, we may speak of each as a T-hour. We shall for brevity refer to mean solar time as S-time. Suppose, now, that we have two clocks, each marked with 360°, or 24 hours, and that the hand of the first, or S-clock, goes round once in 24 S-hours, and that of the second, or T-clock, goes round once in twenty-four T-hours, and suppose that the two clocks are started at 0° or 0h at noon of the initial day. For the sake of distinctness, let us imagine that a T-hour is longer than an S-hour, so that the T-clock goes slower than the S-clock. The measurements of the tide curve give us the height of water exactly at each S-hour; and it is required from these data to determine the height of water at each T-hour. For this end we are, in fact, instructed to count T-time, but are only allowed to do so by reference to S-time, and, moreover, the time is always to be specified as an integral number of hours. Commencing with 0h of the first day, we begin counting 0, 1, 2, &c., as the T-hand comes up to its hour-marks. But, as the S-hand gains on the T-hand, there will come a time when, the T-hand being exactly at the p hour-mark, the S-hand is nearly as far as 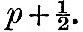 When however, the T-hand has advanced to the p +1 hour-mark, the S-hand will be a little beyond When however, the T-hand has advanced to the p +1 hour-mark, the S-hand will be a little beyond 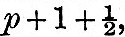 —that is to say, a little less than half an hour before p + 2. Counting, then, in T-time by reference to S-time, we jump from p to p + 2. The counting will go on continuously for a number of hours nearly equal to 2p, and then another number will be dropped, and so on throughout the whole year. If it had been the T-hand which went faster than the S-hand, it is obvious that one number would be repeated at two successive hours instead of one being dropped. We may describe each such process as a "change." —that is to say, a little less than half an hour before p + 2. Counting, then, in T-time by reference to S-time, we jump from p to p + 2. The counting will go on continuously for a number of hours nearly equal to 2p, and then another number will be dropped, and so on throughout the whole year. If it had been the T-hand which went faster than the S-hand, it is obvious that one number would be repeated at two successive hours instead of one being dropped. We may describe each such process as a "change."
Now, if we have a sheet marked for entry of heights of water according to T-hours from results measured at S-hours. we must enter the S-measurements continuously up to p, and we then come to a change; dropping one of the S-series, we go on again continuously until another change, when another is dropped; and so on. Since a change occurs at the time when a T-hour falls almost exactly half-way between two S-hours, it will be more accurate at a change to insert the two S-entries which fall on each side of the truth. If this be done the whole of the S series of measurements is entered on the T-sheet. Similarly, if it be the T-hand which goes faster than the S-hand, we may leave a gap in the T-series instead of duplicating an entry. For the analysis of the T-tide there is therefore prepared a sheet arranged in rows and columns; each row corresponds to one T-day, and the columns are marked 0h, 1h , . . . 23h ; the 0’s may be called T noons. A dot is put in each space for entry, and where their is a change two dots are put if there is to be a double entry, and a bar if there is to be no entry. [Footnote 366-3] The numbers entered in each column are summoned; the results are then divided, each by the proper divisor for its column, and thus the mean value for that column is obtained. In this way 24 numbers are found which give the mean height of water at each of the 24 special hours. If is obvious that if this process were continued over a very long time we should in the end extract the tide under analysis from amongst all the others; but, as the process only extends over about a year, the elimination of the others is not complete. The elimination of the effects of the other tides may be improved by choosing the period for analysis not exactly equal to one year.
Let us now return to our general notation, and consider the 24 mean values, each pertaining to the 24 T-hours. We suppose that all the tides except the T-tide are adequately eliminated, and, in fact, a computation of the necessary corrections for the absence of complete elimination, which is given in the Tidal Report to the British Association in 1872, shows that this is the case. It is obvious that any one of the 24 values does not give the true height of the T-tide at that T-hour, but gives the average height of the water, as due to the T-tide, estimated over half a T-hour before and half a T-hour after that hour. A consideration of this point shows that certain augmenting factors, differing slightly from unity, must be applied. In the reduction of the S-series of tides, the numbers treated are the actual heights of the water exactly at the S-hours, and therefore no augmenting factor is requisite.
We must now explain how the harmonic analysis, which the use of these factors presupposes, is carried out.
If t denotes T-time expressed in T-hours, and n is 15°, we express the height h, as given by the averaging process above explained, by the formula
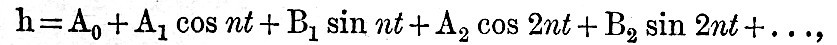
where t is 0, 1, 2,…..23. Then, if Σ denotes summation of the series of 24 terms found by attributing to t its 24 values, it is obvious that
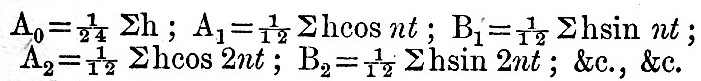
Since n is 15° and t is an integer, it follows that all the cosines and sines involved in these series are equal to one of the following, viz , 0, ±sin 15°, ±sin 30°, ±sin 45°, ±sin 60°, ±sin75, ±1. It is found convenient to denote these sines by 0, ±S1, ±S2, ±S3, ±S4, S5, ±1. The multiplication of the 24 h’s by the various S’s and the subsequent additions may be arranged in a very neat tabular form like that given in a Report to the British Association in 1883. The A’s and B’s having been thus deduced, we have 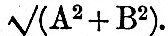 R must then be multiplied by the augmenting factor. We thus have the augmented R. Next the angle whose tangent is B/A gives ζ. The addition to ζ of the appropriate V0 + u gives κ, and the multiplication of R by the appropriate 1/f gives H. The reduction is then complete. An actual numerical example of harmonic analysis is given in the Admiralty Scientific Manual (1885) in the article "Tides"; but the process there employed is slightly different from the above, because the series of observations is supposed to be a short one. R must then be multiplied by the augmenting factor. We thus have the augmented R. Next the angle whose tangent is B/A gives ζ. The addition to ζ of the appropriate V0 + u gives κ, and the multiplication of R by the appropriate 1/f gives H. The reduction is then complete. An actual numerical example of harmonic analysis is given in the Admiralty Scientific Manual (1885) in the article "Tides"; but the process there employed is slightly different from the above, because the series of observations is supposed to be a short one.
Footnotes
366-3 A sample page is given in the Report to the Brit. Assoc., 1883.
Read the rest of this article:
Tides - Table of Contents
|