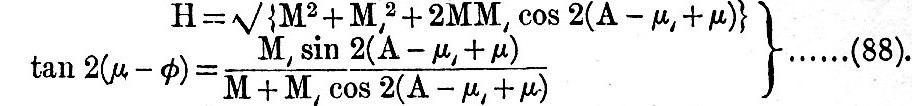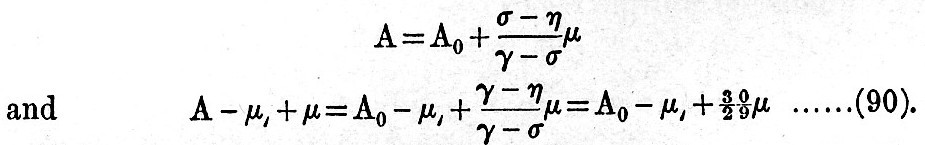V. SYNTHETIC METHOD (cont.)
31. Synthesis of Lunar and Solar Semi-Diurnal Tides
Let A be the excess of  over
over  R.A., so that
R.A., so that
The synthesis is then completed by writing
Then H is the height of the total semi-diurnal tide and φ/(γ - dα/dt) or φ/γ - σ) or 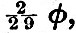 , when φ is given in degrees, is the "interval" from the moon’s transit to high water.
, when φ is given in degrees, is the "interval" from the moon’s transit to high water.
The formulae for H and φ may be written
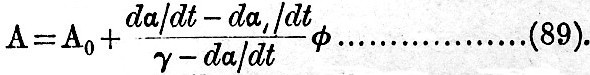
As an approximation we may attribute, to all the quantities in the second term their mean values, and we then have
This approximate formula (90) may be used in computing from (88) the fortnightly inequality in the "height" and "interval."
In this investigation we have supposed that the declinational and parallactic corrections are applied to the lunar and solar tides before their synthesis; but it is obvious that the process might be reversed, and that we may form a table of the fortnightly inequality based on mean values Hm and Hs, and afterwards apply corrections. This is the process usually adopted, but it is less exact. The labour of computing the fortnightly inequality, especially by graphical methods, is not great, and the plan here suggested seems preferable.
Read the rest of this article:
Tides - Table of Contents