V. SYNTHETIC METHOD (cont.)
33. Explanation of Tidal Terms in Common Use; Datum Levels
The mean height at spring tide between high and low water is called the spring rise, and is equal to 2(Hm+Hs). The height between mean high-water mark of neap tide and mean low-water mark at spring tide is called the neap rise, and is equal to 2Hm. The mean height at neap tide between high and low water is called the neap range; this is equal to 2(Hm – Hs). Neap range is usually about one-third of spring range. The mean period between full or change of moon and spring tide is called the age of the tide; this is equal to (κs - κm)/2(σ - η), or, if κs - κm be expressed in degrees, 0h.984 x (κs - κm ); κs - κm is commonly about 36°, and the age about 36h. The period elapsing from the moon’s upper or lower transit until it is high water is called the interval or the lunitidal interval. The interval at full moon or change of moon is called the establishment of the port or the vulgar establishment. The interval at spring tide is called the corrected or mean establishment.
The mean establishment may be found from the vulgar establishment by means of the spring and neap rise and the age of the tide, as follows.
Let α be the age of the tide reduced to angle at the rate of 1º.016 to the hour. Then the mean establishment in hours is equal to the vulgar establishment in hours, diminished by a period expressed in hours numerically equal to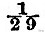 
of the angle whose tangent is Hs sin α/(Hm + Hs cos α), expressed in degrees. Also H8/Hm is equal to the ratio of the excess of spring rise over neap rise to neap rise.
The French have called a quantity which appears to be identical with Hm + Hs, or half the spring rise, the unit of height, and then define the height of any other tide by a tidal coefficient. [Footnote 369-1]
The practice of the British Admiralty is to refer their soundings and tide-tables to "mean low-water mark of ordinary spring tides." This datum is found by taking the mean of the low-water marks of such observations at spring tide as are available, or, if the observations are very extensive, by excluding from the mean such spring tides as appear to be abnormal, owing to the largeness of the moon’s parallax at the time or any other cause. The Admiralty datum is not, then, susceptible of exact scientific definition; but, when it has once been fixed with reference to a bench mark ashore, it is expedient to adhere to it, by whatever process it was first fixed.
It is now proposed to adopt for any new Indian tidal stations a low-water datum for the tide-table to be called "Indian low-water mark," [Footnote 369-2] and to be defined as Hm+Hs+H″+H0 below mean-water level. Although such a datum is not chosen from any precise scientific considerations, it is susceptible of exact definition, is low enough to exclude almost all negative entries from the table (a sine qua non for a good datum), and will differ but little from the Admiralty datum, however that may be determined. A valuable list of datum levels is given by Mr J. Shoolbred in a Report to the British Association in 1879.
Footnotes
369-1 See Hatt, Phénomène des Marées, p. 151, Paris, 1885.
369-2 See Prefaces to Indian Official Tide-Tables for 1887.
Read the rest of this article:
Tides - Table of Contents