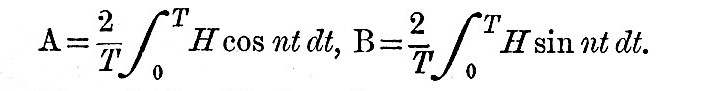VI. TIDAL INSTRUMENTS AND TIDAL PREDICTION (cont.)
37. The Harmonic Analyser
If a function H be expressed as a series of harmonic terms, and if one pair of these terms be A cos nt + B sin nt, then, if T be a multiple of the complete period 2π/n, we have
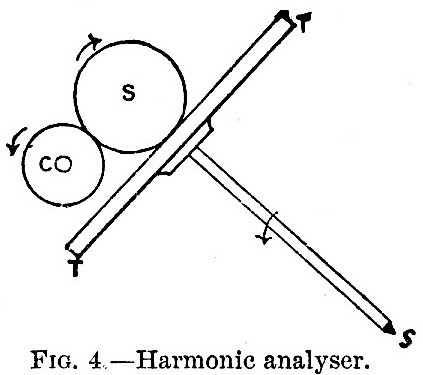
In fig. 4 let TT″ be a circular table, capable of rotation about the inclined shaft s. Let S be a sphere touching the table anywhere along its horizontal diameter. Let C be a cylinder, of somewhat smaller diameter than the sphere, capable of rotation about a horizontal axis parallel to the table, and touching the sphere so that CS is parallel to TT″. Suppose that the point of contact of the sphere with the table is distant x from the centre of the table, and nearer to us than the shaft; then, when the shaft s and the table TT″ turn in such a direction that T rises from the paper and T″ goes below it, the sphere will turn in the direction of its arrow. If the radius of the sphere is a, and that of the cylinder b, then, when the table turns through a small angle δθ, the sphere turns through xδθ/a and the cylinder through xδθ/b. This angle vanishes if S touches the table at the centre, and is reversed if the sphere be moved across to the other side of the centre. Also whilst the table is turning the sphere may be rolled backwards and forwards without rubbing, and thus transmits motion from the table to the cylinder without slipping. Now suppose the turning of the table is so constrained that δθ = k cos ψdψ, whilst x is constrained to be equal to the arbitrarily varying quantity H. Then the total angle turned through by the cylinder, as the machine runs, is proportional to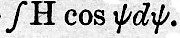 
If we impart to the table a simple harmonic oscillatory motion, with a period proportional to the lunar half-day, whilst the sphere moves, relatively to the centre of the table, proportionately to the tide-heights on the same time-scale then, at the end of a sufficient number of lunar days, we shall find that the total angle turned through by the cylinder is proportional to either the A or B component of the lunar semi-diurnal tide. An index, which points to a dial, may be fixed to the cylinder, so that the required result may be read off.
In the harmonic analyser the tide-curve diagram is wrapped on a drum, which is turned by one hand, whilst with the other a pointer is guided to follow the tide-curve. As the drum turns proportionately to mean solar time, appropriate gearing causes two tables to execute harmonic oscillations in phases at right angles, with lunar semi-diurnal period. At the same time a fork attached to the pointer guides the two spheres so that their distances from the centres of their tables are equal to the tide-height in the diagram. The indexes attached to the two cylinders give the two components of the lunar semi-diurnal tide, and the approximation improves the longer the tide-curve which is passed through the machine. Corresponding to each of the principal lunar and solar tides there are a pair of tables, spheres with guiding forks, and cylinders similarly geared, and there is another sphere and another table, which last always turns the same way and at the same rate as the drum, from which the mean height of water is determined. Such an instrument has been constructed under the supervision of Sir W. Thomson, but has not yet been put into practical use, so that we cannot say how it will compete with the arithmetical harmonic analysis. A similar, but less complex machine for the analysis of meteorological observations is in constant use in the Meteorological Office in London, and is found to work well. [Footnote 371-2]
Footnote
371-2 For further details, see Appendixes iii., iv., v., to Thomson and Tait’s Nat. Phil., 1879, vol. i., part i.; James Thomson, Proc. Roy. Soc., vol. xxiv., 1876, p. 262, and (Sir W. Thomson) pp. 269, 271; Sir W, Thomson, Proc. Inst C.E., vol. lxv.
Read the rest of this article:
Tides - Table of Contents
