1902 Encyclopedia > Tides > [Tidal Instruments and Tidal Prediction] The Tide-Predicting Instrument
Tides
(Part 38)
VI. TIDAL INSTRUMENTS AND TIDAL PREDICTION (cont.)
38. The Tide-Predicting Instrument
The first suggestion for instrumental prediction of tides was given, we believe, by Sir W. Thomson in 1872, and the instruments since made have been founded on the principles which he then laid down. Mr Edward Roberts bore a very important part in the first practical realization of such a machine, and a tide-predicter was constructed by Légé for the Indian Government under his direction. Thomson’s is the only instrument in Europe as yet in regular practical use for navigational purposes. It requires much skill and care in manipulation, and it has been ably worked by Mr Roberts for the production of the Indian tide-tables ever since its completion. We refer the reader to Sir W. Thomson’s paper on "Tidal Instruments," in Inst. C.E., vol. lxv., and to the subsequent discussion, for a full account of the several instruments, and for details of the share borne by the various persons concerned in the realization of the idea.
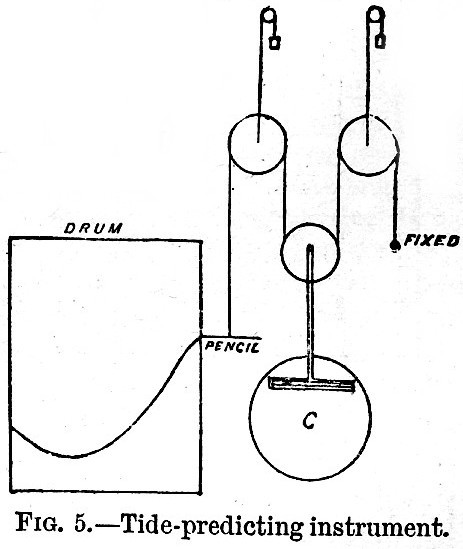
Fig. 5 illustrates diagrammatically the nature of the instrument. A cord passes over and under a succession of pulleys, being fixed at one end and having at the other a pen which touches a revolving drum. If all the pulleys but one be fixed, and if that one executes a simple harmonic motion up and down, the pen will execute the same motion with half amplitude. If a second pulley be now given an harmonic motion, the pen takes it up also with half amplitude. The same is true if all the pulleys are in harmonic motion. Thus the pen sums them all up, and leaves a trace on the revolving drum. When the drum and pulleys are so geared that the angular motion of the drum is proportional to mean solar time, whilst the harmonic motions of the pulleys correspond in range and phase to all the important lunar and solar tides, the trace on the drum is a tide-curve, from which a tide-table may be constructed. The harmonic motion of the pulley is given by an arrangement indicated only in the case of the lower pulley in the figure. The pulley frame has attached to its vertical portion a horizontal slot, in which slides a pin fixed to a wheel. Suppose that whilst tin-drum turns through 15º the wheel turns through 28°·984. Now a lunar day is 24·842 mean solar hours; hence as the drum turns through 15° x 24·842 the wheel turns through 24·842 x 28º·984 or 720º. Thus, if the drum turns with an angular velocity proportional to solar time, the wheel turns with twice the angular velocity proportional to lunar time, and the pulley reared to the wheel executes lunar semi-diurnal harmonic oscillations. When the throw of the pin and its angular position on its wheel are adjusted so as to correspond with the range and phase of the observed lunar semi-diurnal tide, the oscillation of the pulley remains rigorously accurate for that tide for all future tune, it the gearing be rigorously accurate, and with all needful accuracy for some ten years of tide with gearing as practically constructed. The upper pulleys have to be carefully counterpoised as indicated. It has not been found that any appreciable disturbance is caused by the inertia of the moving parts, even when the speed of working is high. The predicter of the India Office takes about four hours to run off a year’s tides but greater speed seems attainable by modification in the on gearing. The Indian instrument, in the store department at Lambeth, has pulleys for the following tides (see chap. iv.):—M2, M4, M6, K1, S1, S2, O, N, P, K2, Q, ν, J, L, λ, 2MS, 2SM, MS, Ssa, Sa.
Read the rest of this article:
Tides - Table of Contents
|
