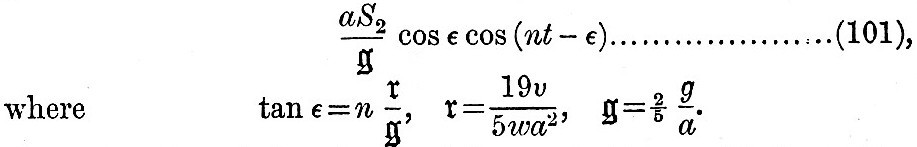1902 Encyclopedia > Tides > [Tidal Deformation of the Solid Earth] Viscous and Elastico-Viscous Tides
Tides
(Part 45)
VIII. TIDAL DEFORMATION OF THE SOLID EARTH (cont.)
45. Viscous and Elastico-Viscous Tides
It might be supposed that the earth is composed of a viscous fluid of great stiffness, or that it possesses an elasticity which breaks down under continued stress. Both these hypotheses have been considered, and the results are confirmatory of the conclusion that the earth is made of very stiff material. [Footnote 374-6] These problems appear to have been worthy of attack, although the existence of measurable oceanic tides of long period negatives the adoption of the hypothesis of true viscosity, at least under stresses comparable with tide-generating forces.
If a sphere of radius a, density w, viscosity modulus υ, be under the action of forces due to a potential per unit volume wr2S2 cos nt, so that n is the speed of the tide, the solution of the problem shows that the tide of the sphere is expressed by
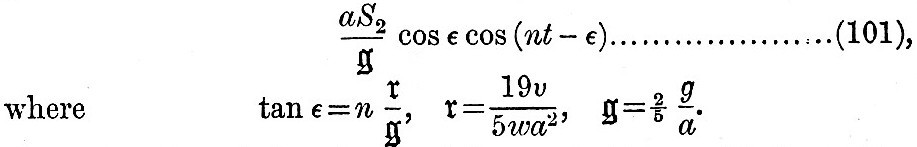
Thus the tides of the viscous globe are to the equilibrium tides of a fluid globe as 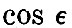 to unity, and there is a retardation to unity, and there is a retardation 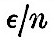 of the time of high tide after the passage of the tide-generator over the meridian. Further, by arguments similar to that applied in the case of elastic tides, it is found that oceanic tides are reduced by the yielding in the proportion of sin of the time of high tide after the passage of the tide-generator over the meridian. Further, by arguments similar to that applied in the case of elastic tides, it is found that oceanic tides are reduced by the yielding in the proportion of sin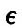 to unity, and that there is an apparent acceleration of the time of high water by to unity, and that there is an apparent acceleration of the time of high water by 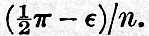 It appears by numerical calculation that, in order that the oceanic semi-diurnal tide may have a value equal to two thirds of the full amount on a rigid globe, the stiffness of the globe must be about twenty thousand times as great as that of pitch at freezing temperature, when it is hard and brittle. We must here pass by the results of the hypothesis of an elasticity degrading under the influence of continued stress. It appears by numerical calculation that, in order that the oceanic semi-diurnal tide may have a value equal to two thirds of the full amount on a rigid globe, the stiffness of the globe must be about twenty thousand times as great as that of pitch at freezing temperature, when it is hard and brittle. We must here pass by the results of the hypothesis of an elasticity degrading under the influence of continued stress.
Footnote
374-6 G. H. Darwin, Phil. Trans., pt. i., 1879, p. 1; see also Lamb, "On the Oscilliations of a Viscous Spheroid," Proc. Lond. Math. Soc., Nov. 1881, p. 51.
Read the rest of this article:
Tides - Table of Contents
|