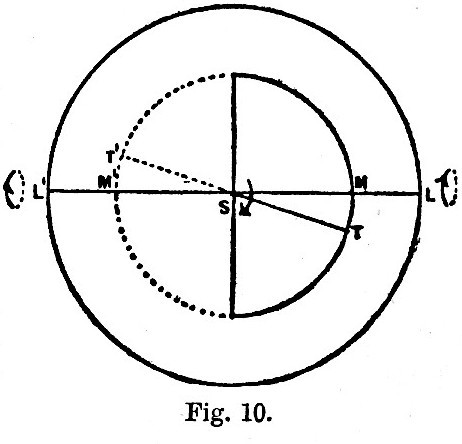
We shall show that if the tidal retardation be small the obliquity of the ecliptic increases, the earth’s rotation is retarded, and the moon’s distance and periodic time are increased. Fig. 10 represents the earth as seen from above the south-pole, so that S is the pole and the outer circle the equator. The earth’s rotation is in the direction of the curved arrow at S. The half of the inner circle which is drawn with a full line is a semi-small-circle of south latitude, and the dotted semicircle is a semi-small-circle in the same north latitude. Generally dotted lines indicate parts of the figure which are below the plane of the paper. It will make the explanation somewhat simpler if we suppose the tides to be raised by a moon and anti-moon diametrically opposite to one another. Let M and M′ be the projections of the moon and anti-moon on to the terrestrial sphere. If the fluid in which the tides are raised were perfectly frictionless, [Footnote 377-5] or if the earth were a perfect fluid or perfectly elastic, the apices of the tidal spheroid would be at M and M′. If, however, there is internal friction, due to any sort of viscosity, the tides will lag, and we may suppose the tidal apices to be at T and T′. Now suppose the tidal protuberances to be replaced by two equal heavy particles at T and T′, which are instantaneously rigidly connected with the earth. Then the attraction of the moon on T is greater than on T′, and that of the anti-moon on T′ is greater than on T. The resultant of these forces is clearly a pair of forces acting on the earth in the direction TM, T′M′. These forces clearly cause a couple about the axis in the equator, which lies in the same meridian as the moon and anti-moon. The direction of the couple is shown by the curved arrows at L,L′. If the effects of this couple be compounded with the existing rotation of the earth according to the principle of the gyroscope, the south pole S tends to approach M and the north pole to approach M′. Hence, supposing the moon to move in the ecliptic, the inclination of the earth’s axis to the ecliptic diminishes, or the obliquity increases. Next the forces TM, T′M′ clearly produce, as in the simpler case considered above, a couple about the earth’s polar axis, which tends to retard the diurnal rotation.
This general explanation remains a fair representation of the state of the case so long as the different harmonic constituents of the aggregate tide-wave do not suffer very different amounts of retardation; and this is the case so long as the viscosity is not great. The rigorous result for a viscous planet shows that in general the obliquity will increase, and it appears that, with small viscosity of the planet if the period of the satellite be longer than two periods of rotation of the planet, the obliquity increases, and vice versa. Hence zero obliquity is only dynamically stable when the period of the satellite is less than two periods of the planet’s rotation.
Suppose the motions of the planet and of its solitary satellite to be referred to the invariable plane of the system. The axis of resultant moment of momentum is normal to this plane, and the component rotations are that of the planet about its axis of figure and the orbital motion of the planet and satellite round their common centre of inertia; the axis of this latter rotation is clearly the normal to the satellite’s orbit. Hence the normal to the orbit, the axis of resultant moment of momentum, and the planet’s axis of rotation must always lie in one plane. From this it follows that the orbit and the planet’s equator must necessarily have a common node on the invariable plane. If either of the component rotations alters in amount or direction, a corresponding change must take place in the other, such as will keep the resultant moment of momentum constant in direction and magnitude. It has been shown that the effect of tidal friction is to increase the distance of the satellite from the planet, and to transfer moment of momentum from that of planetary rotation to that of orbital motion. If, then, the direction of the planet’s axis of rotation does not change, it follows that the normal to the lunar orbit must approach the axis of resultant moment of momentum. By drawing a series of parallelograms on the same diameter and keeping one side constant in direction, this may be easily seen to be true. This is equivalent to saying that the inclination of the satellite’s orbit will decrease. But this decrease of inclination does not always necessarily take place, for the previous investigations show that another effect of tidal friction may be to increase the obliquity of the planet’s equator to the invariable plane, or in other words, to increase the inclination of the planet’s axis to the axis of resultant moment of momentum. Now, if a parallelogram be drawn with a constant diameter, it is seen that by increasing the inclination of one of the sides to the diameter (and even decreasing its length) the inclination of the other side to the diameter may also be increased. The most favourable case for such a change is when the side whose inclination is increased is nearly as long as the diameter. From this it follows that the inclination of the satellite's orbit to the invariable plane may increase, and that it is most likely to increase, when the moment of momentum of planetary rotation is large compared with that of the orbital motion. The analytical solution of the problem agrees with these results, for it shows that if the viscosity of the planet be small the inclination of the orbit always diminishes, but if the viscosity be large, and if the satellite moves with a short periodic time (as estimated in rotations of the planet), the inclination of the orbit will increase. These results convey some idea of the physical causes which may have given rise to the present inclination of the lunar orbit to the ecliptic. For the analytical investigation shows that the inclination of the lunar orbit to a certain plane, which replaces the invariable plane when the solar attraction is introduced, was initially small, that it then increased to a maximum, and that it finally diminished and is still diminishing.
But the laws above referred to would, by themselves, afford a very unsatisfactory explanation of the inclination of the lunar orbit, because the sun’s attraction is a matter of much importance. It has been found that, if the viscosity of the planet be small, the inclination of the orbit of the solitary satellite to the invariable plane will always diminish; but, when solar influence is introduced, the corresponding statement is not true with regard to the inclination of the lunar orbit to the proper plane, for during one part of the moon’s history the inclination to the proper plane would have increased even if the viscosity of the earth had been small.
Consider a satellite revolving about a planet in an elliptic orbit, with a periodic time which is long compared with the period of rotation of the planet; and suppose that frictional tides are raised on the planet. The major axis of the tidal spheroid always points in advance of the satellite, and exercises on it a force which tends to accelerate its linear velocity. When the satellite is in perigee the tides are higher, and this disturbing force is greater than when the satellite is in apogee. The disturbing force may therefore be represented as a constant force, always tending to accelerate the motion of the satellite, and as a periodic force which accelerates in perigee and retards in apogee. The constant force causes a secular increase of the satellite’s mean distance and a retardation of its mean motion. The accelerating force in perigee causes the satellite to swing out further than it would otherwise have done, so that when it comes round to apogee it is more remote from the planet. The retarding force in apogee acts exactly inversely, and diminishes the perigean distance. Thus, the apogean distance increases and the perigean distance diminishes, or, in other words, the eccentricity of the orbit increases. Now consider another case, and suppose the satellite’s periodic time to be identical with that of the planet’s rotation. Then, when the satellite is in perigee, it is moving faster than the planet rotates, and when in apogee it is moving slower; hence at apogee the tides lag, and at perigee they are accelerated. Now the lagging apogean tides give rise to an accelerating force on the satellite, and increase the perigean distance, whilst the accelerated perigean tides give rise to a retarding force, and decrease the apogean distance. Hence in this case the eccentricty of the orbit will diminish. It follows from these two results that there must be some intermediate periodic time of the satellite for which the eccentricity does not tend to vary.
But the preceding general explanation is in reality somewhat less satisfactory than it seems, because it does not make clear the existence of certain antagonistic influences, to which, however, we shall not refer. The rigorous result, for a viscous planet, shows that in general the eccentricity of the orbit will increase; but, it the obliquity of the planet's equator be nearly 90°, or if the viscosity be so great as to approach perfect rigidity, or if the periodic time of the satellite (measured in rotations of the planet) be short, the eccentricity will slowly diminish. When the viscosity is small the law of variation of eccentricity is very simple: if eleven periods of the satellite occupy a longer time than eighteen rotations of the planet, the eccentricity increases, and vice versa. Hence in the case of small viscosity a circular orbit is only dynamically stable if the eleven periods are shorter than the eighteen rotations.
Footnotes
377-4 These explanations, together with other remarks, are to be found in the abstracts of Mr G. H. Darwin’s memoirs in Proc. Roy. Soc., 1878 to 1881.
377-5 We here suppose the tides not to be inverted. If they are inverted the conclusion is precisely the same.
Read the rest of this article:
Tides - Table of Contents